


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-2-2019
Date: 13-2-2019
Date: 13-2-2019
|
Given two functions 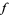 and
and 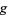 analytic in
analytic in 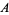 with
with 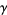 a simple loop homotopic to a point in
a simple loop homotopic to a point in 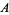 , if
, if 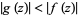 for all
for all 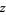 on
on 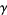 , then
, then 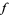 and
and 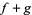 have the same number of roots inside
have the same number of roots inside 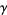 .
.
A stronger version has been proved by Estermann (1962). The strong version also has a converse, as shown by Challener and Rubel (1982).
REFERENCES:
Challener, D. and Rubel, L. "A Converse to Rouché's Theorem." Amer. Math. Monthly 89, 302-305, 1982.
Estermann, T. Complex Numbers and Functions. London: Oxford University Press, p. 156, 1962.
Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, p. 111, 1996.
Krantz, S. G. "Rouché's Theorem." §5.3.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 74, 1999.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., p. 22, 1975.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|