A polynomial is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. A polynomial in one variable (i.e., a univariate polynomial) with constant coefficients is given by

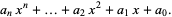(1)

The individual summands with the coefficients (usually) included are called monomials (Becker and Weispfenning 1993, p. 191), whereas the products of the form 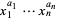 in the multivariate case, i.e., with the coefficients omitted, are called terms (Becker and Weispfenning 1993, p. 188). However, the term "monomial" is sometimes also used to mean polynomial summands without their coefficients, and in some older works, the definitions of monomial and term are reversed. Care is therefore needed in attempting to distinguish these conflicting usages.

The highest power in a univariate polynomial is called its order, or sometimes its degree.

Any polynomial 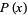 with 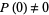 can be expressed as

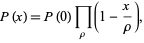(2)

where the product runs over the roots 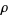 of 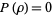 and it is understood that multiple roots are counted with multiplicity.

A polynomial in two variables (i.e., a bivariate polynomial) with constant coefficients is given by

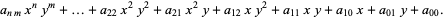(3)

The sum of two polynomials is obtained by adding together the coefficients sharing the same powers of variables (i.e., the same terms) so, for example,

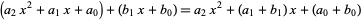(4)

and has order less than (in the case of cancellation of leading terms) or equal to the maximum order of the original two polynomials. Similarly, the product of two polynomials is obtained by multiplying term by term and combining the results, for example

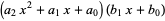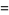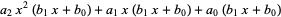			(5)
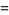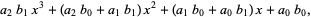			(6)

and has order equal to the sum of the orders of the two original polynomials.

A polynomial quotient

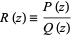(7)

of two polynomials 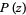 and 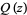 is known as a rational function. The process of performing such a division is called long division, with synthetic division being a simplified method of recording the division.

For any polynomial 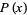,  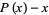divides 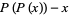, meaning that the polynomial quotient is a rational polynomialor, in the case of an integer polynomial, another integer polynomial (N. Sato, pers. comm., Nov. 23, 2004).

Exchanging the coefficients of a univariate polynomial end-to-end produces a polynomial

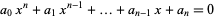(8)

whose roots are reciprocals 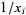 of the original roots .

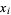Horner's rule provides a computationally efficient method of forming a polynomial from a list of its coefficients, and can be implemented in the Wolfram Language as follows.

  Polynomial[l_List, x_] := Fold[x #1 + #2&, 0, l]

The following table gives special names given to polynomials of low orders.

Polynomials of fourth degree may be computed using three multiplications and five additions if a few quantities are calculated first (Press et al. 1989):

(9)

where

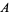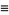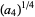			(10)
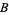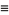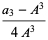			(11)
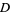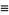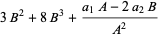			(12)
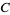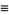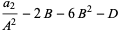			(13)
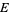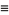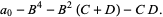			(14)

Similarly, a polynomial of fifth degree may be computed with four multiplications and five additions, and a polynomial of sixth degree may be computed with four multiplications and seven additions.

Polynomials of orders one to four are solvable using only rational operations and finite root extractions. A first-order equation is trivially solvable. A second-order equation is soluble using the quadratic equation. A third-order equation is solvable using the cubic equation. A fourth-order equation is solvable using the quartic equation. It was proved by Abel and Galois using group theory that general equations of fifth and higher order cannot be solved rationally with finite root extractions (Abel's impossibility theorem).

However, solutions of the general quintic equation may be given in terms of Jacobi theta functions or hypergeometric functions in one variable. Hermite and Kronecker proved that higher order polynomials are not soluble in the same manner. Klein showed that the work of Hermite was implicit in the group properties of the icosahedron. Klein's method of solving the quintic in terms of hypergeometric functions in one variable can be extended to the sextic, but for higher order polynomials, either hypergeometric functions in several variables or "Siegel functions" must be used (Belardinelli 1960, King 1996, Chow 1999). In the 1880s, Poincaré created functions which give the solution to the 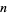th order polynomial equation in finite form. These functions turned out to be "natural" generalizations of the elliptic functions.

REFERENCES:

Barbeau, E. J. Polynomials. New York: Springer-Verlag, 1989.

Becker, T. and Weispfenning, V. Gröbner Bases: A Computational Approach to Commutative Algebra. New York: Springer-Verlag, 1993.

Belardinelli, G. "Fonctions hypergéométriques de plusieurs variables er résolution analytique des équations algébriques générales." Mémoral des Sci. Math. 145, 1960.

Bini, D. and Pan, V. Y. Polynomial and Matrix Computations, Vol. 1: Fundamental Algorithms. Boston, MA: Birkhäuser, 1994.

Borwein, P. and Erdélyi, T. Polynomials and Polynomial Inequalities. New York: Springer-Verlag, 1995.

Chow, T. Y. "What is a Closed-Form Number." Amer. Math. Monthly 106, 440-448, 1999.

Cockle, J. "Notes on the Higher Algebra." Quart. J. Pure Applied Math. 4, 49-57, 1861.

Cockle, J. "Notes on the Higher Algebra (Continued)." Quart. J. Pure Applied Math. 5, 1-17, 1862.

King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.

Mignotte, M. and Stefănescu, D. Polynomials: An Algorithmic Approach. Singapore: Springer-Verlag, 1999.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, 1989.

Project Mathematics. "Polynomials." Videotape. http://www.projectmathematics.com/polynom.htm.

Ram, R. "Sums of Powers." http://users.tellurian.net/hsejar/maths/sumsofpowers/.

Weisstein, E. W. "Books about Polynomials." http://www.ericweisstein.com/encyclopedias/books/Polynomials.html.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد