

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Orthogonal Polynomials
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
"Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
الجزء والصفحة:
...
13-2-2019
19461
Orthogonal Polynomials
Orthogonal polynomials are classes of polynomials {p_n(x)}" src="http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline1.gif" style="height:15px; width:43px" /> defined over a range
![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline2.gif) that obey an orthogonalityrelation
that obey an orthogonalityrelation
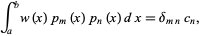 |
(1) |
where 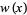 is a weighting function and
is a weighting function and 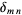 is the Kronecker delta. If
is the Kronecker delta. If 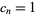 , then the polynomials are not only orthogonal, but orthonormal.
, then the polynomials are not only orthogonal, but orthonormal.
Orthogonal polynomials have very useful properties in the solution of mathematical and physical problems. Just as Fourier series provide a convenient method of expanding a periodic function in a series of linearly independent terms, orthogonal polynomials provide a natural way to solve, expand, and interpret solutions to many types of important differential equations. Orthogonal polynomials are especially easy to generate using Gram-Schmidt orthonormalization.
A table of common orthogonal polynomials is given below, where 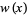 is the weighting function and
is the weighting function and
![c_n=int_a^bw(x)[p_n(x)]^2dx](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/NumberedEquation2.gif) |
(2) |
(Abramowitz and Stegun 1972, pp. 774-775).
| polynomial | interval | 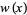 |
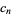 |
| Chebyshev polynomial of the first kind | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline9.gif) |
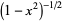 |
|
| Chebyshev polynomial of the second kind | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline12.gif) |
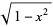 |
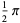 |
| Gegenbauer polynomial | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline15.gif) |
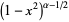 |
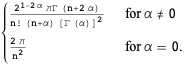 |
| Hermite polynomial | 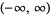 |
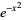 |
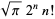 |
| Jacobi polynomial | 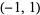 |
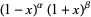 |
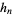 |
| Laguerre polynomial | 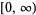 |
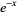 |
1 |
| generalized Laguerre polynomial | 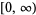 |
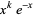 |
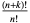 |
| Legendre polynomial | ![[-1,1]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline29.gif) |
1 | 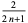 |
In the above table,
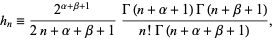 |
(3) |
where 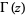 is a gamma function.
is a gamma function.
The roots of orthogonal polynomials possess many rather surprising and useful properties. For instance, let 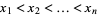 be the roots of the
be the roots of the 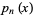 with
with 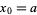 and
and 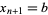 . Then each interval
. Then each interval ![[x_nu,x_(nu+1)]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline36.gif) for
for 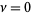 , 1, ...,
, 1, ..., 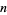 contains exactly one root of
contains exactly one root of 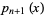 . Between two roots of
. Between two roots of 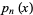 there is at least one root of
there is at least one root of 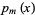 for
for 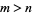 .
.
Let 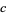 be an arbitrary real constant, then the polynomial
be an arbitrary real constant, then the polynomial
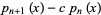 |
(4) |
has 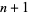 distinct real roots. If
distinct real roots. If 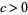 (
(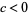 ), these roots lie in the interior of
), these roots lie in the interior of ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline47.gif) , with the exception of the greatest (least) root which lies in
, with the exception of the greatest (least) root which lies in ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline48.gif) only for
only for
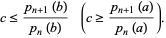 |
(5) |
The following decomposition into partial fractions holds
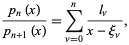 |
(6) |
where {xi_nu}" src="http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline49.gif" style="height:15px; width:23px" /> are the roots of
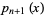 and
and
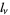 |
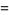 |
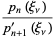 |
(7) |
 |
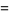 |
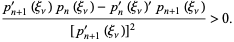 |
(8) |
Another interesting property is obtained by letting {p_n(x)}" src="http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline57.gif" style="height:15px; width:43px" /> be the orthonormal set of polynomials associated with the distribution
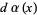 on
on ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline59.gif) . Then the convergents
. Then the convergents 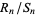 of the continued fraction
of the continued fraction
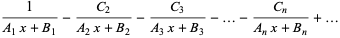 |
(9) |
are given by
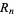 |
 |
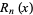 |
(10) |
 |
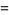 |
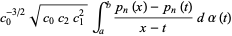 |
(11) |
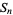 |
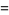 |
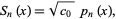 |
(12) |
where 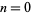 , 1, ... and
, 1, ... and
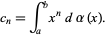 |
(13) |
Furthermore, the roots of the orthogonal polynomials 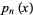 associated with the distribution
associated with the distribution 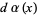 on the interval
on the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline73.gif) are real and distinct and are located in the interior of the interval
are real and distinct and are located in the interior of the interval ![[a,b]](http://mathworld.wolfram.com/images/equations/OrthogonalPolynomials/Inline74.gif) .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.
Arfken, G. "Orthogonal Polynomials." Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 520-521, 1985.
Chihara, T. S. An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, 1978.
Gautschi, W.; Golub, G. H.; and Opfer, G. (Eds.) Applications and Computation of Orthogonal Polynomials, Conference at the Mathematical Research Institute Oberwolfach, Germany, March 22-28, 1998. Basel, Switzerland: Birkhäuser, 1999.
Iyanaga, S. and Kawada, Y. (Eds.). "Systems of Orthogonal Functions." Appendix A, Table 20 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1477, 1980.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 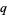 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S. Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992.
Sansone, G. Orthogonal Functions. New York: Dover, 1991.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 44-47 and 54-55, 1975.
 الاكثر قراءة في مواضيع عامة في الجبر
الاكثر قراءة في مواضيع عامة في الجبر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















