AC Method
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
17-1-2019
1359
AC Method
The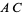 
method is an algorithm for factoring quadratic polynomials of the form 
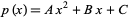with integercoefficients. As its name suggests, the crux of the algorithm is to consider the multiplicative factors of the product of the coefficients 
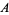and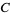 
. More precisely, the goal is to find an integer pair 
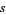and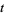 
satisfying 
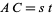and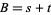 
simultaneously, whereby one can rewrite 
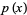in the form
 |
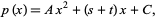(1)
|
and to factor the remaining four-term polynomial by grouping into a product of linear factors with integer coefficients.
For example, consider the polynomial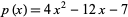 
having coefficients 
, 
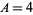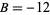, and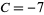 
. To begin the 
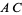factorization, consider the product 
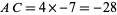. By observation, 
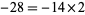while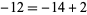 
; in particular, this guarantees that 
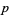can be rewritten so that
 |
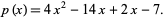(2)
|
This four-term expression for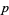 
can be factored by grouping:
 |
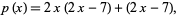(3)
|
and so
 |
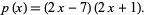(4)
|
One can easily see that the above method generalizes to certain polynomials of the form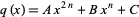 
for positive integers 
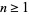, though the result will be a factorization into pairs of polynomials of degree 
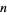which aren't necessarily linear.
This procedure is an alternative to the more straightforward utilization of the quadratic formula and has a number of drawbacks. For example, finding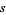 
and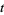 
hinges on observation and/or guess-and-check; this can be particularly problematic when the product 
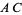has a large number of factors. Moreover, while the quadratic formula illustrates immediately the existence of irrational and/or imaginary roots, the 
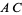method often disguises such behavior and thus requires a degree of "pre-processing," e.g., by analyzing the polynomial discriminant.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
