
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-7-2018
Date: 18-7-2018
Date: 18-7-2018
|
In parabolic cylindrical coordinates, the scale factors are 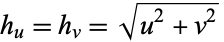 ,
, 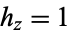 and the separation functions are
and the separation functions are 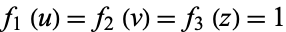 , giving Stäckel determinant of
, giving Stäckel determinant of 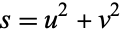 . the Helmholtz differential equation is
. the Helmholtz differential equation is
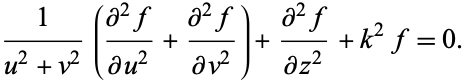 |
(1)
|
attempt separation of variables by writing
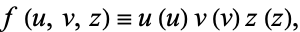 |
(2)
|
then the Helmholtz differential equation becomes
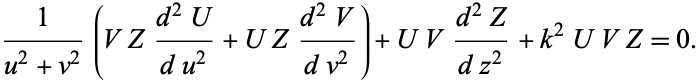 |
(3)
|
Divide by 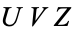 ,
,
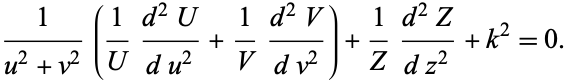 |
(4)
|
Separating the 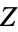 part,
part,
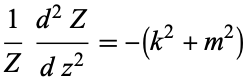 |
(5)
|
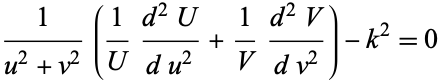 |
(6)
|
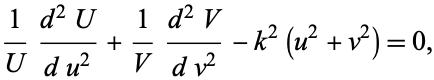 |
(7)
|
so
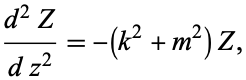 |
(8)
|
which has solution
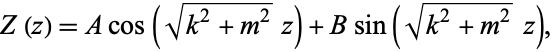 |
(9)
|
and
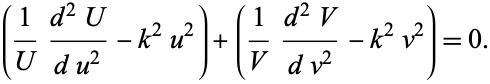 |
(10)
|
This can be separated
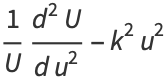 |
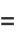 |
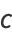 |
(11)
|
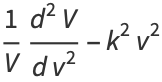 |
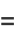 |
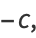 |
(12)
|
so
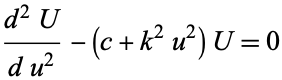 |
(13)
|
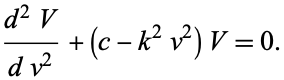 |
(14)
|
These are the Weber differential equations, and the solutions are known as Parabolic Cylinder Functions.
REFERENCES:
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, p. 36, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 515 and 658, 1953.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|