Homogeneous Ordinary Differential Equation

A linear ordinary differential equation of order 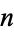 is said to be homogeneous if it is of the form

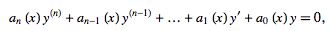(1)

where 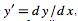  , i.e., if all the terms are proportional to a derivative of  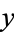(or 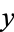 itself) and there is no term that contains a function of  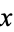alone.

However, there is also another entirely different meaning for a first-order ordinary differential equation. Such an equation is said to be homogeneous if it can be written in the form

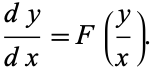(2)

Such equations can be solved in closed form by the change of variables 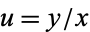 which transforms the equation into the separable equation

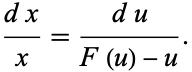REFERENCES:

Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 8th ed. New York: Wiley, pp. 49-50, 2004.