It has been mentioned in the other sections on arithmetic operations that many other logical circuits are known and used for each of the operations discussed. This situation is even more pronounced with respect to multiplication. Since the process itself is more complicated, it is only reasonable that more variations exist for multiplication. Among the many methods, the most frequently used are those which employ the use of an accumulator in one way or another. The following binary multiplication problem illustrates the steps which must be performed by the computer:

The partial products are easy to obtain since they are each either zero or identical to the multiplicand. However, the addition is complicated because the partial products to be accumulated are not simply 3-digit numbers since each successive partial product is shifted one position to the left of the partial product above it. Besides accumulation, then, it is necessary to include a shifting device capable of reproducing the multiplicand in any desired position. The shifting may be done either upon the partial products or upon the number in the accumulator itself, just as long as the digits are aligned properly before each step in the computation.

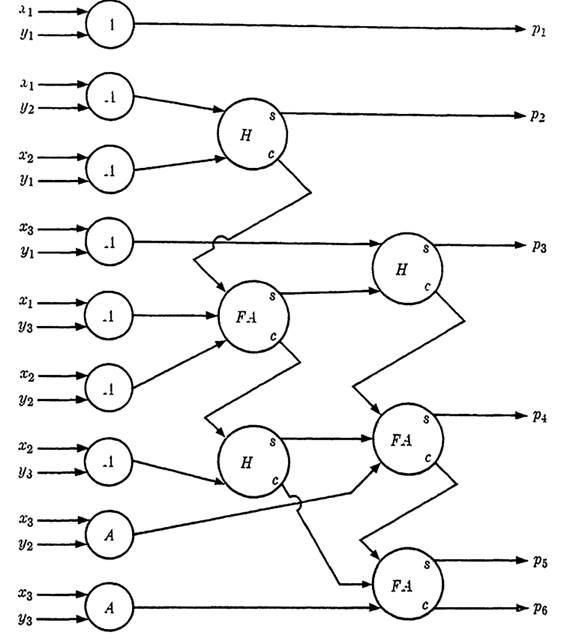
FIG. 1-1. Logical circuit for the simultaneous multiplication of two 3-digit numbers.

The preceding discussion has indicated a way in which the problem of multiplication can be, and usually is, approached. However, rather than introduce the shifting circuits necessary for this approach, we will conclude this chapter with a circuit capable of multiplying two 3-digit numbers directly. This circuit (Fig. 1-1) depends only on logical elements already introduced. Although the circuit is by no means trivially self-evident, a careful consideration of the various paths in connection with the sample problem above should convince the student of the validity of the circuit.  The half adder is used with the notation introduced earlier and, in addition, adder, is used with identical notation except that FA replaces the letter H found in a half adder. The two elements perform in the same way except that a full adder accepts three inputs instead of two. The notation for this circuit is similar to that of the adder circuit given earlier in that the multiplicand and multiplier are X = x₃x₂x₁ and

Y = y₃, y₂,y₁ respectively. The product is denoted by P = P₆P₅P₄P₃P₂P₁. Note that it is possible for the product to have six, but not more than six, digits.

A complete discussion of circuits involved in arithmetic operations would fill a book larger than this one. It is not our purpose to exhaust the subject but merely to pursue it to the point that the student may appreciate the nature of such problems and the role that Boolean algebra can be expected to play in their solution. While it is true that we are, at this point, very far from the complete design of a computer, the principles and methods which have been presented should have prepared the reader to solve many interesting and worthwhile problems with the use of electrical circuits of one type or another.

مواضيع ذات صلة

Zero Polynomial

Kronecker,s Polynomial Theorem

THE ALGEBRA OF SETS-The number of elements in a set

THE ALGEBRA OF SETS-Solution of equations

THE ALGEBRA OF SETS-Conditional equations

THE ALGEBRA OF SETS-Properties of set inclusion

THE ALGEBRA OF SETS- Expanding, factoring, and simplifying

THE ALGEBRA OF SETS-Fundamental laws

THE ALGEBRA OF SETS-Venn diagrams

THE ALGEBRA OF SETS-The combination of sets

THE ALGEBRA OF SETS-Element and set

THE ALGEBRA OF SETS-Introduction