Characteristics of Crisp Set

1.1 Ordinary Characteristics

Let us look over the operational characteristics of union, intersection, and complement set [Table 1.1]. Commutativity of union and intersection is

satisfied as follows

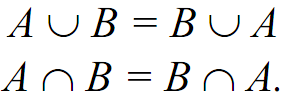
The operations of intersection and union follows the associativity

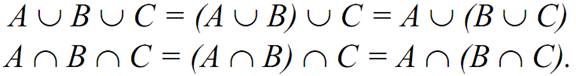
Union or intersection between itselves is reduced to the set itself. This  is ‘idempotency’.

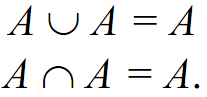
In addition, for union and intersection, the distributivity is held.

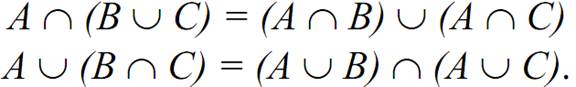
De Morgan’s law is satisfied with the union, intersection and complement operation.

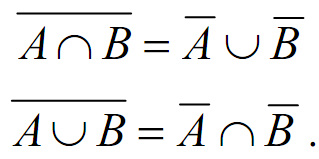
                                               Table 1.1. Features of Crisp Set

                                                                 Table 1.1. (cont’)

1.2 Convex Set

Definition (Convex set) The term convex is applicable to a set A in Rⁿ(n-dimensional Euclidian vector space) if the followings are satisfied.

i) Two arbitrary points s and r are defined in A.

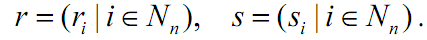
(N is a set of positive integers)

ii) For arbitrary real number  λ between 0 and 1, point t is involved in A where t is

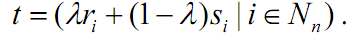
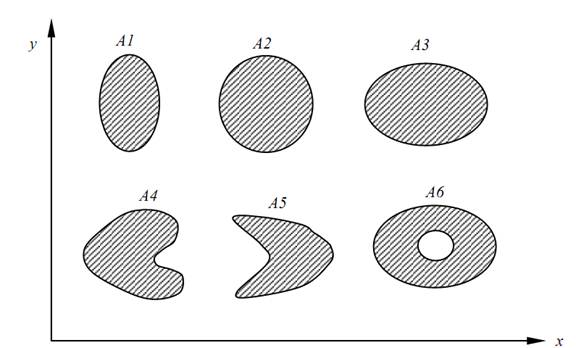
                Fig. 1.1. Convex sets A1, A2, A3 and non-convex sets A4, A5, A6 in |R²

In other wads, if every point on the line connecting two points s and r in  A is also in A. (Fig 1.1) shows some examples of convex and non-convex

Sets

____________________________________________________________________________________________________

Kwang H. Lee, First Course on Fuzzy Theory and Applications, 2005, Springer, pag(5-7)

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

THE OPERATION OF FUZZY SET -Standard Operations of Fuzzy Set

FUZZY SETS-Expanding Concepts of Fuzzy Set

FUZZY SETS-Definition of Fuzzy Set

FUZZY SETS-Operation of Sets

FUZZY SETS-Sets