Sets

1.1 Elements of Sets

An universal set X is defined in the universe of discourse and it includes all possible elements related with the given problem. If we define a set A in

the universal set X, we see the following relationships

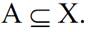
In this case, we say a set A is included in the universal set X. If A is not included in X, this relationship is represented as follows.

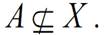
If an elementx is included in the setA, this element is called as a member of the set and the following notation is used.

                                                                                             x ∊ A.

If the elementx is not included in the setA, we use the following notation.

                                                                                           x ∉ A.

In general, we represent a set by enumerating its elements. For example, elements a₁, a₂, a₃,….., a_n are the elements of set A, it is represented as

                                                                                     A = {a₁ , a₂ ,….. , a_n }.

Another representing method of sets is given by specifying the conditions of elements. For example, if the elements of set B should satisfy

the conditions P₁, P₂,….., P_n, then the set B is defined by the following.

                                                                         B = {b | b satisfies p₁, p ₂,…. , p_n }.

In this case the symbol “|” implies the meaning of “such that”.

1.2 Relation between Sets

A set consists of sets is called a family of sets. For example, a family set containing sets A₁, A₂,….is represented by

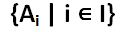
where i is a set identifier and I is an identification set. If all the elements in set A are also elements of set B, A is a subset of B.

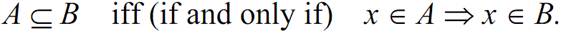
The symbol  ⟹means  “implication”. If the following relation is  satisfied,

                                                 A ⊆ B  and B ⊆A

A andB have the same elements and thus they are the same sets. This relation is denoted by

                                                                    A = B

If the following relations are satisfied between two sets A and B,

                                                                 A Ž⊆ B  and A ≠ B

then B has elements which is not involved in A. In this case, A is called a proper subset of B andthis relation is denoted by

                                                                            A ⊂ B

A set that has no element is called an empty set ⏀‡. An empty set can be a subset of any set.

1.3 Membership

If we use membership function (characteristic function or discrimination function), we can represent whether an element x is involved in a set A or not.

Definition (Membership function) For a set A, we define a membership function 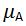maps the elements in the universal set X to the set {0,1}.

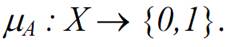
As we know, the number of elements in a setA is denoted by the cardinality |A|. A power set P(A) is a family set containing the subsets of

set A. Therefore the number of elements in the power set P(A) is represented by

|P(A)| = 2^|A| .

Example 1.1 If A = {a, b, c}, then |A| = 3

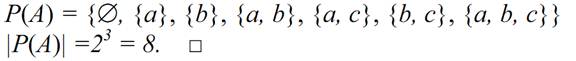
Kwang H. Lee, First Course on Fuzzy Theory and Applications, 2005, Springer,pag(1-3)

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

THE OPERATION OF FUZZY SET -Standard Operations of Fuzzy Set

FUZZY SETS-Expanding Concepts of Fuzzy Set

FUZZY SETS-Definition of Fuzzy Set

FUZZY SETS-Characteristics of Crisp Set

FUZZY SETS-Operation of Sets