We conclude by showing that even fair elections can produce unexpected results.

Consider a political party convention at which five different voting schemes are adopted. Assume that there are 110 delegates to this national convention,  at which five of the party members, denoted by A, B, C, D, and E, have been nominated as the party’s presidential candidate. Each delegate must rank all five candidates according to his or her choice. Although there are 5! =: 5 × 4 × 3 × 2×1 = 120 possible rankings, many fewer will appear in practice because electors typically split into blocs with similar rankings. Let’s assume that our 110 delegates submit only six different preference lists, as indicated in the following preference profile:

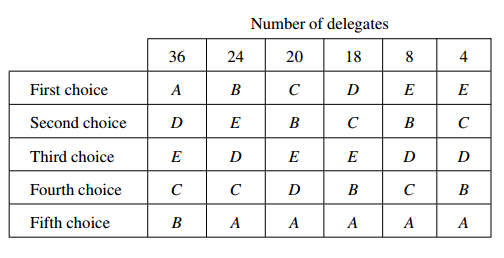
The 36 delegates who most favor nominee A rank D second, E third, C fourth,  and B fifth. Although A has the most first-place votes, he is actually ranked last by the other 74 delegates. The 12 electors who most favor nominee E split into two subgroups of 8 and 4 because they differ between B andC on their second and fourth rankings.

We shall assume that our delegates must stick to these preference schedules throughout the following five voting agendas. That is, we will not allow any delegate to switch preference ordering in order to vote in a more strategic manner or because of new campaigning.

We report the results when six popular voting methods are used. There are six different results.

1. Majority. As one might expect with five candidates, there is no majority winner.

2. Plurality. If the party were to elect its candidate by a simple plurality, nominee A would win with 36 first-place votes, in spite of the fact that A was favored by less than one-third of the electorate and was ranked dead last by the other 74 delegates.

3. Runoff. On the other hand, if the party decided that a runoff election should be held between the top two contenders (A and B), who together received a majority of the first-place votes in the initial plurality ballot, then candidate B outranks A on 74 of the 110 preference schedules and is declared the winner in the runoff.

4. Hare Method. Suppose the Hare method is used: a sequence of ballots is held,  and eliminating at each stage the nominee with the fewest first-place votes. The last to survive this process becomes the winning candidate. In our example E,  with only 12 first-place votes, is eliminated in the first round. E can then be deleted from the preference profile, and all 110 delegates will vote again on successive votes. On the second ballot, the 12 delegates who most favored E earlier now vote for their second choices, that is, 8 for B and 4 for C; the number of first-place votes for the four remaining nominees is

Thus, D is eliminated. On the third ballot the 18 first-place votes for D are reassigned to C, their second choice, giving

Now B is eliminated. On the final round, 74 of the 110 delegates favor C over A,  and therefore C wins.

5. Borda Count. Given that they have the complete preference schedule for each delegate, the party might choose to use a straight Borda count to pick the winner.

They assign five points to each first-place vote, four points for each second, three points for a third, two points for a fourth, and one point for a fifth. The scores are:

A: 254 = (5)(36)+(4)(0)+(3)(0)+(2)(0)+(1)(24+20+18+8+4)

B: 312 = (5)(24)+(4)(20+8)+(3)(0)+(2)(18+4)+(1)(36)

C: 324 = (5)(20)+(4)(18+4)+(3)(0)+(2)(36+24+8)+(1)(0)

D: 382 = (5)(18)+(4)(36)+(3)(24+8+4)+(2)(20)+(1)(0)

E: 378 = (5)(8+4)+(4)(24)+(3)(36+20+18)+(2)(0)+(1)(0)

The highest total score of 382 is achieved by D, who then wins. A has the lowest score (254) and B the second lowest (312).

6. Condorcet. With five candidates, there is often no Condorcet winner. However,  when we make the head-to-head comparisons, we see that E wins out over:

• A by a vote of 74 to 36

• B by a vote of 66 to 44

• C by a vote of 72 to 38

• D by a vote of 56 to 54

So there is a Condorcet winner, namely E.

مواضيع ذات صلة

Remez Algorithm

Quadratic Phase Array

Fractional Fourier Transform

Circulant Matrix

Logistic Map--r=-2

Logistic Map--r=2

Logistic Map--r=4

Lotka-Volterra Equations

Population Growth

Survivorship Curve

Tent Map

Traveling Salesman Problem