The term strategic voting means voting in a way that does not represent your actual preferences, in order to change the result of the election. We would call the resulting ballot insincere.

Suppose your favorite is candidate X. (We will call you an X supporter.) Then X would normally appear at the top of your preference list. But sometimes you can achieve X’s election by voting for another candidate in first place! This is most common in runoff situations; you can ensure that your candidate does not have to face a difficult opponent. The following example illustrates this.

Sample Problem 1.1 A runoff election has preference profile

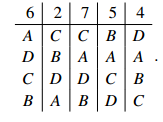
Show that the supporters of C can change the result so that their candidate wins,  by the two voters in the second column changing their ballots by demoting their candidate.

Solution. Initially the first-place votes are A–6, B–5,C–9, D–4, so runoff election will be between A and C, and A wins 15–9. The revised profile is

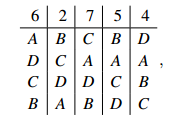
the first-place votes are A–6, B–7, C–7, D–4, so the runoff election is between B and C, and C wins 13–11.

Even when you cannot ensure victory for your favorite candidate, you may still be able to obtain a preferable result. For example, suppose you support candidate X;  you think candidate Y is acceptable, but hate candidate Z. Even if insincere voting cannot ensure victory for candidate X, you may be able to swing the election to Y rather than Z.

Sample Problem 1.2 An election with four candidates and seven voters is to be decided by the Hare system. The preference profile is

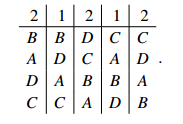
Show that one of the two voters with B,A,D,C can change the outcome to a more favorable one by insincere voting.

Solution. First consider the result of sincere voting. Initially A is eliminated,  having no first-place votes:

The winner is C.

Now suppose one voter changes his ballot from B,A,D,C to D,A,B,C. The profile is

The winner is D. This is a preferable outcome for the voter who switched.

Your Turn. Consider a Hare system election with preference profile

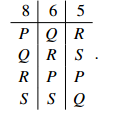
Show that P would win this election. Show that if one of the six supporters of Q changes her vote, she could ensure that R wins, even though a majority of voters still prefer Q to R.

مواضيع ذات صلة

Remez Algorithm

Quadratic Phase Array

Fractional Fourier Transform

Circulant Matrix

Logistic Map--r=-2

Logistic Map--r=2

Logistic Map--r=4

Lotka-Volterra Equations

Population Growth

Survivorship Curve

Tent Map

Traveling Salesman Problem