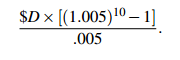You do not normally wait until the end of a loan period to pay back a loan. The usual practice is to pay equal amounts each month (or each week or . . . ). Another situation in which equal deposits are made is the periodic savings account, such as a Christmas club or retirement account, where a fixed amount is deposited into savings each period.

Regular Savings

Consider a periodic savings account. Suppose you deposit $D each month. The interest each month is M%; write m = M/100. Assume the account is empty to start, and you pay in for n months. (Often n = 11 or 12, because people use these accounts to save for vacations or Christmas shopping.)

The calculations to find the amount at the end of the n-th month might start:

This soon becomes complicated. An easier way is to calculate the effect of putting each new payment in a new bank account. The total in all the accounts at the end of n months will be the required amount.

Payment 1 draws interest for n months, so the amount in that account at the end is $D(1 + m)n; payment 2 draws interest for n − 1 months, so the amount in that account at the end is $D(1+m)ⁿ⁻¹. The total of accounts 1 and 2 is

We call this amount the accumulation.

Sample Problem 1.1 At the beginning of each month you put $100 into an account that pays 6% annual interest. How much have you accumulated at the end of the year?

Solution. 6% annual interest is .5% per month. So m = .005,n = 12,D = 100,  and you get

                      $100(1.005¹³−1.005)/.005

                       = $100(1.066986−1.005)×200

                       = $20000(0.061986)

                       = $1239.72

Some investment funds are set up so that you make your payment at the end of the payment period, rather than the beginning. In these cases it is usual to add the last payment to the accumulation, even though it accrues no interest. In that case the accumulation is

For example, in a Christmas club, you might make your first payment on January 31st and withdraw the money late in November. There are ten payments. If the annual interest is again 6%, your accumulation is

مواضيع ذات صلة

Remez Algorithm

Quadratic Phase Array

Fractional Fourier Transform

Circulant Matrix

Logistic Map--r=-2

Logistic Map--r=2

Logistic Map--r=4

Lotka-Volterra Equations

Population Growth

Survivorship Curve

Tent Map

Traveling Salesman Problem