
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
التدفق المغناطيسي ( الفيض)
المؤلف:
فريدريك بوش ، دافيد جيرد
المصدر:
اساسيات الفيزياء
الجزء والصفحة:
17-1-2016
28718
التدفق المغناطيسي ( الفيض)
لقد فسر فاراداي القوة الدافعة الكهربية المستحثة في ملف ما بدلالة كمية تسمى التدفق المغناطيسي. ومن أجل هذا ، ابتكر قاعدة تحدد كيفية رسم خريطة لخطوط المجال المغناطيسي. فإذا كان للمجال المغناطيسي في منطقة ما مقدار هو B فإننا نمثل هذا المقدار بيانياً بأن نتفق على رسم خطوط المجال وهي على أبعاد معينة من بعضها البعض ، وأن تمثل المجالات الأضعف بخطوط متباعدة عن بعضها البعض بشكل أكبر. وبعبارة أخرى يمكن القول بأن كثافة خطوط المجال في الرسم تتناسب مع قيمة B.
ويمكننا قياس كثافة الخطوط هذه لو أقمنا سطحاً متعامداً مع الخطوط ثم قمنا بعد الخطوط التي تخترق وحدة المساحات من هذا السطح ؛ كما في الشكل (1)، حيث يمر ستة عشر خطاً من خطوط المجال خلال مساحة قدرها 1 m2. وقد نود أن نختار كثافة الخطوط هذه لتمثل شدة مجال مغناطيسي ولتكن 1 T مثلاً. ومن ثم فإن منطقة تمر بوحدة المساحات بها ثمانية خطوط ستمثل شدة مجال مقدارها النصف أي 0.5 T ، أما المنطقة التي بها 32 خطاً في المرت المربع فإنها تمثل مجالاً شدته 2T وهكذا. أي أن التمثيل البياني للمجال المغناطيسي هو ان B تتناسب مع كثافة خطوط الفيض ، او مع عدد خطوط المجال التي تعبر مساحة ما مقسوما على تلك المساحة.
ويؤدي هذا التفسير إلى اعتبار أن عدد الخطوط المارة خلال المسافة A يمثل المقدارB┴A وهذا هو ما يسمى الفيض ( التدفق) المغناطيسي خلال A ، وعادة ما يعبر عنه بالرمز Φ:
(1) الفيض المغناطيسي خلالB┴A = Φ = A
ومن الواضح أن وحدات SI للفيض المغناطيسي ستكونT.m2 ونختصر هذه الوحدة في اسم خاص هو الوبر weber (Wb). وهكذا.
1 Wb = 1 T.m2
أو بدلاً من ذلك 1 T = 1Wb/m2
وبسبب هذا التعبير الأخير فإن المجال المغناطيسي B يشار إليه أحياناً بأنه كثافة الفيض ( التدفق).
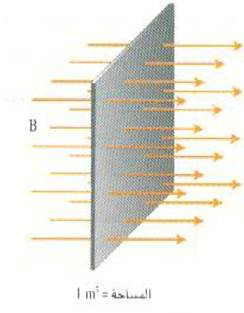
الشكل (1): سنتفق على رسم عدد خطوط المجال المغناطيسي بحيث يتناسب مع مقدار B ويخترق وحدة المساحات المتعامدة مع خطوط المجال.
ومن المهم جداً تذكر أننا اعتبرنا B متعامداً مع مستوى المساحة A في الشكل (2 أ) فإذا أدرنا المساحة A كما في الشكل (2 ب) فإنه لن تمر خلالها أية خطوط للمجال ولهذا فإن = 0Φ. وقد يكون الفيض سالباً كذلك كما هو موضح في الشكل (2 جـ) حيث يتخذ كل من B و n اتجاهين متضادين وهناك طريقة بسيطة لكتابة هذه العلاقة بين Φ والاتجاه وذلك بوصف اتجاه العمود n ، المقام على المساحة A. والمركبةB┴ = B cos θ هي مركبة B الموازية للعمود. وعلى هذا تكون المعادلة العامة للفيض المغناطيسي هي :
(2) Φ = (B cos θ)A = BA cos θ
حيث θ هي الزاوية المحصورة بين B وn.
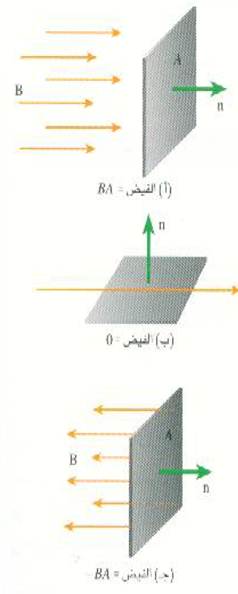
الشكل ((2: يعتمد الفيض خلال مساحة ما على الاتجاهات النسبية بين المساحة وخطوط المجال.
 الاكثر قراءة في الكهرومغناطيسية
الاكثر قراءة في الكهرومغناطيسية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















