Exact and inexact differentials
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص57-59
2025-11-03
34
Exact and inexact differentials
Consider a system undergoing the changes depicted in Fig. 2.20. The initial state of the system is i and, in this state, the internal energy is Ui. Work is done by the system as it expands adiabatically to a state f. In this state the system has an internal energy Uf and the work done on the system as it changes along Path 1 from i to f is w. Notice our use of language: U is a property of the state; w is a property of the path. Now consider another process, Path 2, in which the initial and final states are the same as those in Path 1 but in which the expansion is not adiabatic. The internal energy of both the initial and the final states are the same as before (because U is a state function). However, in the second path an energy q′ enters the system as heat and the work w′ is not the same as w. The work and the heat are path functions. In terms of the mountaineering analogy in Section 2.2, the change in altitude (a state function) is independent of the path, but the distance travelled (a path function) does depend on the path taken between the fixed endpoints. If a system is taken along a path (for example, by heating it), U changes from Ui to Uf, and the overall change is the sum (integral) of all the infinitesimal changes along the path:
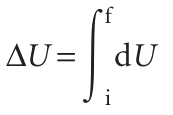
The value of ∆U depends on the initial and final states of the system but is independent of the path between them. This path-independence of the integral is expressed by saying that dU is an ‘exact differential’. In general, an exact differential is an infinitesimal quantity that, when integrated, gives a result that is independent of the path between the initial and final states. When a system is heated, the total energy transferred as heat is the sum of all individual contributions at each point of the path:
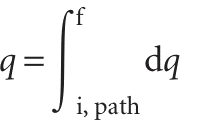
Notice the difference between this equation and eqn 2.38. First, we do not write ∆q, because q is not a state function and the energy supplied as heat cannot be expressed as qf − qi. Secondly, we must specify the path of integration because q depends on the path selected (for example, an adiabatic path has q ≠ 0, whereas a nonadiabatic path between the same two states would have q ≠ 0). This path-dependence is expressed by saying that dq is an ‘inexact differential’. In general, an inexact differential is an infinitesimal quantity that, when integrated, gives a result that depends on the path between the initial and final states. Often dq is written dq to emphasize that it is in exact and requires the specification of a path. The work done on a system to change it from one state to another depends on the path taken between the two specified states; for example, in general the work is different if the change takes place adiabatically and non-adiabatically. It follows that dw is an inexact differential. It is often written pw.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
