Eisenstein,s Irreducibility Criterion
المؤلف:
Childs, L
المصدر:
A Concrete Introduction to Higher Algebra. New York: Springer-Verlag
الجزء والصفحة:
...
19-1-2019
1188
Eisenstein's Irreducibility Criterion
Eisenstein's irreducibility criterion is a sufficient condition assuring that an integer polynomial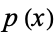 
is irreducible in the polynomial ring ![Q[x]](http://mathworld.wolfram.com/images/equations/EisensteinsIrreducibilityCriterion/Inline2.gif)
.
The polynomial
where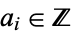 
for all 
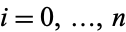and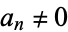 
(which means that the degree of 
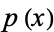is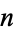 
) is irreducible if some prime number 
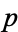divides all coefficients 
, ..., 
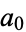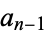, but not the leading coefficient 
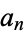and, moreover, 
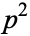does not divide the constant term 
.
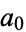This is only a sufficient, and by no means a necessary condition. For example, the polynomial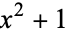 
is irreducible, but does not fulfil the above property, since no prime number divides 1. However, substituting 
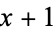for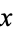 
produces the polynomial 
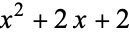, which does fulfill the Eisenstein criterion (with 
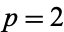) and shows the polynomial is irreducible.
REFERENCES:
Childs, L. A Concrete Introduction to Higher Algebra. New York: Springer-Verlag, pp. 169-172, 1979.
Herstein, I. N. Topics in Algebra, 2nd ed. New York: Wiley, pp. 160-161, 1975.
الاكثر قراءة في مواضيع عامة في الجبر
اخر الاخبار
اخبار العتبة العباسية المقدسة
