Galvanic Cells and Standard Half-Cell Potentials

Here we investigate some of the properties of galvanic cells, cells used to produce an electric potential. Luigi Galvani discovered the first such cell by accident in 1791. Following Galvani's discovery, Alessandro Volta developed a practical cell in 1800, and it was Volta's cell that led to the work of Davy and Faraday.

Consider the electrochemical cell shown in Figure 1-1. Pieces of zinc and copper are immersed, respectively, in solutions of ZnSO₄ and CuSO₄. The solutions are in contact through a glass frit which is sufficiently porous to allow ions to pass through, but which will prevent mixing of the solutions. When a voltmeter is attached between the Zn and Cu electrodes, it is found that an electric potential has developed.

If the voltmeter is replaced by a resistor and an ammeter, it is found that an electric current flows. If, after current has flowed for some time, the electrodes are removed and weighed, it is found that the Zn electrode has lost mass and the Cu electrode has gained mass.

The electrode mass changes are as expected from Faraday's laws if the processes at the Zn and Cu electrodes are the half-reactions:

The overall cell reaction, is a spontaneous process, ΔG° = -212.8 kJ, and it is this spontaneous process which leads to the electric potential.

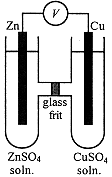
Figure 1-1. A galvanic cell.

An electrochemical cell generates a potential difference E. (The symbol E, commonly used in electrochemistry, refers to electromotive force, an archaic term for potential difference.) The electrical work done when n moles of electrons is passed by the cell can be found using Eq. (1-1), w = -nFE. It can be shown that the electrical work done by an electrochemical cell, at constant temperature and pressure, is equal to the change in Gibbs free energy of the cell components,

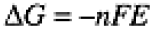                                                      (1.1)

If the cell reaction is spontaneous, ΔG < 0 and E > 0, hence the negative sign in Eq. (1-1). Combining Eqs. (1-1) and (1-2), we have the Nernst equation, which relates E to the reaction quotient Q:

                                (1.2)

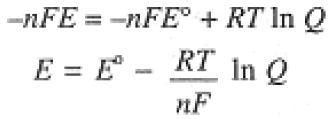                               (1.3)

where E° = -DG°/nF is the standard potential of the cell, i.e., the potential of the cell when all species are in standard states. We sometimes use the Nernst equation with T = 298 K and the natural logarithm converted to base 10:

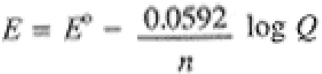                                 (1.4)

Example 1

Compute the potential of the cell shown in Figure 1-1 when T = 298 K, [Cu^₂₊] = 0.010 M, [Zn^₂₊] = 0.0050 M. The standard potential is computed from ΔG°,

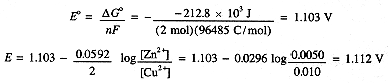
An electrochemical cell reaction, like any oxidation-reduction reaction, can be written as the sum of an oxidation half-reaction and a reduction half-reaction. In the case of a cell, these half-reactions correspond to the reactions at the two electrodes. Since the cell reaction is the sum of the half-cell reactions, it is convenient to think of dividing the cell potential into half-cell potentials. Unfortunately, there is no way of measuring a half-cell potential—we always nee two half-cells to make a cell, the potential of which is measurable. By convention, the half-cell reaction,

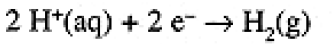                          (1.5)

has been chosen as the primary reference half-cell with standard potential taken to be E° = 0.000 V. Standard half-cell potentials then are determined by cells that include Eq. (1-5) as one of the half-cell reactions. Thus the standard potential of the cell with cell reaction

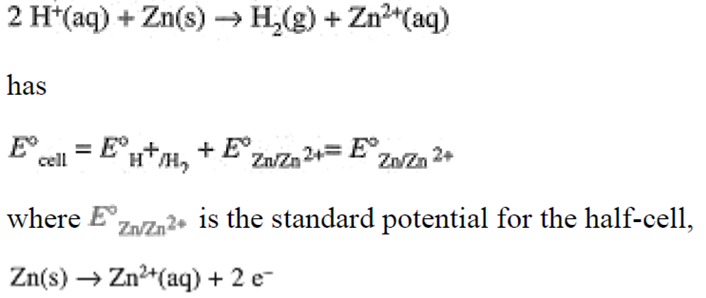
Standard half-cell potentials are usually tabulated as reduction potentials, e.g.,

The corresponding oxidation half-cell potential is the negative of this value, i.e., 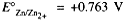 . Standard half-cell potentials can be used to compute standard cell potentials, standard Gibbs free energy changes, and equilibrium constants for oxidation reduction reactions.