Let p: X˜ → X be a covering map over a topological space X. Let f:Z → X be a continuous map from some topological space Z into X. If the topological space Z is locally path-connected then one can formulate a criterion to determine whether or not there exists a map f˜:Z → X˜ for which p ◦f˜ = f . This criterion is stated in terms of the homomorphisms of fundamental groups induced by the continuous maps f:Z → X and p: X˜ → X. We shall use this criterion in order to derive a necessary and sufficient condition for two covering maps over a connected and locally path-connected topological space to be topologically equivalent. We shall also study the deck transformations of a covering space over some connected and locally path-connected topological space.
Lemma 1.18 Let p: X˜ → X be a covering map over a topological space X, let Z be a locally path-connected topological space, and let g:Z → X˜ be a function from Z to X˜. Suppose that p ◦ g:Z → X is continuous, and that g ◦ γ: [0, 1] → X˜ is continuous for all paths γ: [0, 1] → Z in Z. Then the function g is continuous.
Proof Let f:Z → X be the composition function p◦g. Then the function f is a continuous map from Z to X.
Let z be a point of Z. Then there exists an open neighbourhood V of f(z) in X which is evenly covered by the map p. The inverse image p−1 (V ) of V in the covering space X˜ is a disjoint union of open sets, each of which is mapped homeomorphically onto V by p. One of these open sets contains the point g(z), since f(z) = p(g(z)). Let us denote this open set by V˜ . Then g(z) ∈ V˜ , and V˜ is mapped homeomorphically onto V by the map p. Let s: V → V˜ denote the inverse of the restriction (p|V˜ ): V˜ → V of the covering map p to V˜ . Then the map s is continuous, and p(s(v)) = v for all v ∈ V .
Now f−1 (V ) is an open set in Z containing the point z. But the topological space Z is locally path-connected. Therefore there exists a path-connected open set Nz in Z such that z ∈ Nz and Nz ⊂ f−1 (V ). We claim that g(Nz) ⊂ V˜ . Let z΄ be a point of Nz. Then there exists a path γ: [0, 1] → Nz in N from z to z΄ . Moreover f(γ([0, 1])) ⊂ V . Let η: [0, 1] → X˜ be the path in X˜ defined such that η(t) = s(f(γ(t))) for all t ∈ [0, 1]. Then η([0, 1]) ⊂ V˜ , and η is the unique path in X˜ for which η(0) = g(z) and p◦η = f ◦γ. But the composition function g ◦γ is a path in X˜, g(γ(0)) = g(z) and p◦g ◦γ = f ◦γ.
Therefore g ◦ γ = η. It follows that g(γ([0, 1])) ⊂ V˜ , and therefore g(z΄) ∈ V˜ .
This proves that g(Nz) ⊂ V˜ . Moreover g(z΄) = s(f(z΄)) for all z΄∈ Nz, and therefore the restriction g|Nz: Nz → X˜ of the function g to the open set Nz is continuous.
We have now shown that, given any point z of Z, there exists an open set Nz in Z such that z ∈ Nz and the restriction g|Nz of g:Z → X˜ to Nz is continuous. It follows from this that the function g is continuous on Z.
Indeed let U be an open set in X˜. Then g−1(U) ∩ Nz is an open set for all z ∈ Z, since g|Nz is continuous. Moreover g−1 (U) is the union of the open sets g−1(U) ∩ Nz as z ranges over all points of Z. It follows that g−1 (U) is itself an open set in Z. Thus g:Z → X˜ is continuous, as required.
Theorem1.19 Let p: X˜ → X be a covering map over a topological space X, and let f:Z → X be a continuous map from some topological space Z into X. Suppose that the topological space Z is both connected and locally path-connected. Suppose also that
f# (π1(Z, z0)) ⊂ p#(π1(X˜, x˜0)),
where z0 and x˜0 are points of Z and X˜ respectively which satisfy f(z0) = p(x˜0). Then there exists a unique continuous map f˜:Z → X˜ for which f˜ (z0) = x˜0 and p ◦f˜ = f.
Proof Let P denote the set of all ordered pairs (α, ρ), where α: [0, 1] → Z is a path in Z with α(0) = z0, ρ: [0, 1] → X˜ is a path in X˜ with ρ(0) = x˜0, and f ◦ α = p ◦ ρ. We claim that there is a well-defined function f˜:Z → X˜ characterized by the property that f˜ (α(1)) = ρ(1) for all (α, ρ) ∈ P.
The topological space Z is path-connected, by Proposition 1.14. Therefore, given any point z of Z, there exists a path α in Z from z0 to z. Moreover it follows from the Path Lifting Theorem that, given any path α in Z from z0 to z there exists a unique path ρ in X˜ for which ρ(0) = x ˜0 and p ◦ ρ = f ◦α. It follows that, given any element z of Z, there exists some element (α, ρ) of P for which α(1) = z.
Let (α, ρ) and (β, σ) be elements of P. Suppose that α(1) = β(1). Then [(f ◦α).(f ◦ β)−1] = f#[α.β−1]. But f#(π1(Z, z0)) ⊂ p#(π1(X˜, x˜0). Therefore [(f ◦ α).(f ◦ β)−1] ∈ p#(π1(X˜, x˜0)). It follows from Corollary 1.5 that ρ(1) =σ(1). We conclude therefore that if (α, ρ) and (β, σ) are elements of P, and if α(1) = β(1), then ρ(1) = σ(1). This establishes the existence of a unique function f˜:Z → X˜ characterized by the property that f˜ (α(1)) = ρ(1) for all (α, ρ) ∈ P. Now p(ρ(1)) = f(α(1)) for all (α, ρ) ∈ P, and therefore p◦f˜ = f.
Also f˜(z0) = ˜x0, since (εz0, εx˜0 ) ∈ P, where εz0 denotes the constant path in Z based at z0 and εx˜0 denotes the constant path in X˜ based at x˜0. Thus it only remains to show that the map f˜:Z → X˜ is continuous. In view of Lemma 1.18, it suffices to show that f˜ maps paths in Z to paths in X˜.
Let γ: [0, 1] → Z be a path in Z. We claim that the composition function f˜◦ γ is continuous, and is thus a path in X˜. Let α be a path in Z from z0 to γ(0), let ρ: [0, 1] → X˜ be the unique path in X˜ satisfying ρ(0) = x˜0 and p ◦ ρ = f ◦ α, and let σ: [0, 1] → X˜ be the unique path in X˜ satisfying σ(0) = ρ(1) and p ◦ σ = f ◦ γ. Now, for each τ ∈ [0, 1], there is a path ατ : [0, 1] → Z from z0 to γ(τ ) defined such that
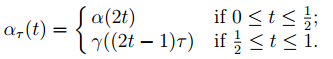
Then f ◦ ατ (t) = p ◦ ρτ (t) for all t ∈ [0, 1] where ρτ : [0, 1] → X˜ is the path in X˜ from x˜0 to σ(τ ) defined such that
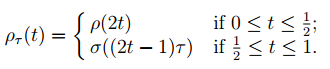
It follows that (ατ , ρτ ) ∈ P, for all τ ∈ [0, 1], and therefore f˜ (γ(τ )) = f˜ (ατ (1)) = ρτ (1) = σ(τ ) for all τ ∈ [0, 1]. Thus f˜ ◦ γ = σ. We conclude that f˜◦ γ is a path in X˜ for any path γ in Z. It then follows from Lemma 1.18 that the function f˜:Z → X˜ is a continuous map from Z to X˜ with the required properties.
Corollary 1.20 Let p: X˜ → X be a covering map over a topological space X, and let f:Z → X be a continuous map from some topological space Z into X.
Suppose that the covering space X˜ is path-connected and that the topological space Z is both connected and locally path-connected. Let z0 and w0 be points of Z and X˜ respectively for which f(z0) = p(w0). Then there exists a map f˜:Z → X˜ satisfying p ◦ f˜ = f if and only if there exists a subgroup H of π1(X, p(w0)) such that H is conjugate to p#(π1(X, w˜0)) and f#(π1(Z, z0)) ⊂ H .
Proof Suppose that there exists a map f˜:Z → X˜ for which p ◦f˜ = f.
Then f#(π1(Z, z0)) ⊂ H, where H = p#(π1(X˜,f˜(z0))). Moreover it follows from Lemma 1.7 that the subgroup H of π1(X, p(w0)) is conjugate to p#(π1(X, w˜0)) in π1(X, p(w0)).
Conversely suppose that f#(π1(Z, z0)) ⊂ H, where H is a subgroup of π1(X, p(w0)) that is conjugate to p#(π1(X, w˜0)). It follows from Lemma 1.7 that there exists a point x˜ of X˜ for which p(˜x) = p(w0) and p#(π1(X ˜, x˜)) = H. Then
f# (π1(Z, z0)) ⊂ p#(π1(X˜, x˜)).
It then follows from Theorem 1.19 that there exists a continuous map f˜:Z → X˜ for which p ◦ f˜= f, as required.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


