Proposition 1.1 Let p: X˜ → X be a covering map over a topological space X, let α: [0, 1] → X and β: [0, 1] → X be paths in X, where α(0) = β(0) and α(1) = β(1), and let                         α˜: [0, 1] → X˜ and β˜: [0, 1] → X˜ be paths in X˜ such that p ◦ α˜ = α and p ◦ β˜ = β. Suppose that α˜(0) = β˜(0) and that α ≃ β rel {0, 1}.

Then α˜(1) = β˜(1) and α˜ ≃ β˜ rel {0, 1}.

Proof Let x0 and x1 be the points of X given by

                x₀ = α(0) = β(0), x₁ = α(1) = β(1).

Now α ≅β rel {0, 1}, and therefore there exists a homotopy F: [0, 1]×[0, 1] → X such that F(t, 0) = α(t) and F(t, 1) = β(t) for all t ∈ [0, 1], F(0, τ ) = x₀ and F(1, τ ) = x₁ for all τ ∈         [0, 1].

It then follows from the Monodromy Theorem (The Monodromy Theorem)that there exists a continuous map G: [0, 1] × [0, 1] → X˜ such that p ◦ G = F and G(0, 0) = α˜(0). Then p(G(0, τ )) = x₀ and p(G(1, τ )) = x₁ for all τ ∈ [0, 1].

A straightforward application of (Let p: X~ → X be a covering map, let Z be a connected topological space, and let g:Z → X~ and h:Z → X~ be continuous maps.

Suppose that p ◦g = p ◦ h and that g(z) = h(z) for some z ∈ Z. Then g = h.) shows that any continuous lift of a constant path must itself be a constant path. Therefore G(0, τ ) = x˜₀

and G(1, τ ) = x˜₁ for all τ ∈ [0, 1], where x˜₀ = G(0, 0) = α˜ (0), x˜₁ = G(1, 0).

However

         G(0, 0) = G(0, 1) = ˜x0 = ˜α(0) = β˜(0),

         p(G(t, 0)) = F(t, 0) = α(t) = p(˜α(t))

and

           p(G(t, 1)) = F(t, 1) = β(t) = p(β˜(t))

for all t ∈ [0, 1]. Now Proposition (Let p: X~ → X be a covering map, let Z be a connected topological space, and let g:Z → X~ and h:Z → X~ be continuous maps.  Suppose that p ◦g = p ◦ h and that g(z) = h(z) for some z ∈ Z. Then g = h.)ensures that the lifts α˜and β˜ of the paths α and β are uniquely determined by their starting points. It follows that               G(t, 0) = α˜ (t) and G(t, 1) = β˜(t) for all t ∈ [0, 1]. In particular,  

    α˜(1) = G(0, 1) = x˜₁ = G(1, 1) = β˜(1).

Moreover the map G: [0, 1] × [0, 1] → X˜ is a homotopy between the paths α˜ and β˜ which satisfies G(0, τ ) = x˜₀ and G(1, τ ) = x˜₁ for all τ ∈ [0, 1]. It follows that α˜ ≃β˜                       rel {0, 1}, as required

Corollary 1.2 Let p: X˜ → X be a covering map over a topological space X, and let x˜0 be a point of X˜. Then the homomorphism

          p_#: π₁(X˜, x˜₀) → π₁(X, p(x˜₀))

of fundamental groups induced by the covering map p is injective

Proof Let σ₀ and σ₁ be loops in  X~ based at the point  x~₀, representing elements [σ₀] and [σ1] of π₁(X˜, x˜₀). Suppose that p_#[σ₀] = p_#[σ₁]. Then p◦σ₀ ≃ p ◦ σ₁ rel {0, 1}. Also σ₀(0) = x˜₀ = σ₁(0). Therefore σ₀ ≃σ₁ rel {0, 1}, by Proposition 1.1, and thus [σ₀] = [σ₁]. We conclude that the homomorphism  p_#: π₁(X˜, x˜₀) → π₁(X, p(x˜₀)) is injective

Corollary 1.3 Let p: X˜ → X be a covering map over a topological space X, let x˜₀ be a point of X˜, and let γ be a loop in X based at p(x˜₀). Then  [γ] ∈ p_#(π₁(X˜, x˜₀)) if and only if there exists a loop γ˜ in X˜, based at the point x˜₀, such that p ◦ γ˜ = γ.

Proof If γ = p ◦ γ˜ for some loop γ˜ in X˜ based at x˜₀ then [γ] = p_#[γ˜], and therefore [γ] ∈ p_#(π₁(X˜, x˜₀)).

Conversely suppose that [γ] ∈ p_#(π₁(X˜, x˜₀)). We must show that there exists some loop γ˜ in X˜ based at x˜₀ such that γ = p ◦ γ˜. Now there exists a loop σ in X˜ based at the point x ˜₀ such that [γ] = p_#([σ]) in π₁(X, p(x˜₀)).

Then γ ≃ p ◦ σ rel {0, 1}. It follows from the Path Lifting Theorem for covering maps that there exists a unique path γ˜: [0, 1] → X˜ in X˜ for which γ˜ (0) = x˜₀ and p ◦ γ˜ = γ. It then follows from Proposition 1.1 that γ˜ (1) = σ(1) and γ˜ ≃ σ rel {0, 1}. But σ(1) = x˜₀. Therefore the path γ˜ is the required loop in X˜ based the point x˜₀ which satisfies                  p ◦ γ˜ = γ.

Corollary 1.4 Let p: X˜ → X be a covering map over a topological space X, let w₀ and w₁ be points of X˜ satisfying p(w₀) = p(w₁), and let α: [0, 1] → X˜ be a path in X˜ from w0 to w₁. Suppose that [p ◦ α] ∈ p_#(π₁(X, w˜₀)). Then the path α is a loop in X˜, and thus w₀ = w₁.

Proof It follows from Corollary 1.3 that there exists a loop β based at w0 satisfying p ◦ β = p ◦ α. Then α(0) = β(0). Now Proposition (Let p: X˜ → X be a covering map, let Z be a connected topological space, and let g:Z → X˜ and h:Z → X˜ be continuous maps. Suppose that p ◦ g = p ◦ h and that g(z) = h(z) for some z ∈ Z. Then g = h.) ensures that the lift to X˜ of any path in X is uniquely determined by its starting point. It follows that α = β. But then the path α must be a loop in X˜, and therefore w₀ = w₁, as required.

Corollary 1.5 Let p: X˜ → X be a covering map over a topological space X.  Let α: [0, 1] → X and β: [0, 1] → X be paths in X such that α(0) = β(0) and α(1) = β(1), and let α.β⁻¹ be the loop in X defined such that

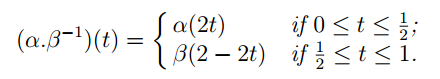
Let α˜: [0, 1] → X˜ and β˜: [0, 1] → X˜ be the unique paths in X˜ such that p ◦ α˜ = α, and p ◦ β˜ = β. Suppose that α˜(0) = β˜(0). Then α˜(1) = β˜(1) if and only if                                [α.β⁻¹] ∈ p_#(π₁(X˜, x˜₀)), where x˜₀ = α˜(0) = β˜(0).

Proof Suppose that α˜(1) = β˜(1). Then the concatenation α˜.β˜⁻¹ is a loop in X˜ based at x˜₀, and [α.β⁻¹] = p_#([α˜.β˜⁻¹]), and therefore [α.β⁻¹] ∈ p_#(π₁(X ˜, x˜₀)).  Conversely suppose that α˜ and β˜ are paths in X˜ satisfying p ◦ α˜ = α,  p ◦ β˜ = β and α˜(0) = β˜(0) = x˜₀, and that [α.β⁻¹] ∈ p_#(π₁(X˜, x˜₀)). We must show that α˜(1) = β˜(1). Let γ: [0, 1] → X be the loop based at p(x˜₀) given by γ = α.β⁻¹. Thus

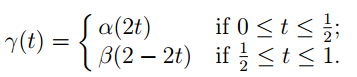
Then [γ] ∈ p_#(π₁(X˜, x˜₀)). It follows from Corollary 1.3 that there exists a loop γ˜ in X˜ based at x˜₀ such that p ◦ γ˜ = γ. Let αˆ: [0, 1] → X˜ and Let βˆ: [0, 1] → X˜ be the paths in X˜ defined such that αˆ (t) = γ˜ (1/2t)    and    βˆ(t) = γ˜ (1 −1/2t) for all t ∈ [0, 1]. Then

           α˜(0) = αˆ (0) = β˜(0) = βˆ(0) = x˜₀,  p ◦ αˆ = α = p ◦ α˜ and p ◦ βˆ = β = p ◦ β˜.

But Proposition (Let p: X˜ → X be a covering map, let Z be a connected topological space, and let g:Z → X˜ and h:Z → X˜ be continuous maps. Suppose that p ◦ g = p ◦ h and that g(z) = h(z) for some z ∈ Z. Then g = h.) ensures that the lift to X˜ of any path in X is uniquely determined by its starting point.

Therefore α˜ = α ˆand β˜ = βˆ. It follows that

α˜(1) = α(1ˆ) = γ˜ (1/2) = βˆ(1) = β˜(1),

as required.

Theorem 1.6 Let p: X˜ → X be a covering map over a topological space X.

Suppose that X˜ is path-connected and that X is simply-connected. Then the covering map p: X˜ → X is a homeomorphism.

Proof We show that the map p: X˜ → X is a bijection. This map is surjective  (since covering maps are by definition surjective). We must show that it is injective. Let w₀ and w₁ be points of X˜ with the property that p(w₀) = p(w₁). Then there exists a path α: [0, 1] → X˜ with α(0) = w0 and α(1) = w₁, since X˜ is path-connected. Then p ◦ α is a loop in X based at the point x₀, where x₀ = p(w₀). However π₁ (X,p(w₀)) is the trivial group, since X is simply- connected. It follows from Corollary 1.4 that the path α is a loop in X˜ based at w₀, and therefore w₀ = w₁. This shows that the the covering map p: X˜ → X is injective. Thus the map p: X˜ → X is a bijection, and thus has a well-defined inverse p⁻¹: X → X˜. It now follows from Lemma (Let p: X^~ → X be a covering map. Then p(V ) is open in X  for every open set V in  X^~. In particular, a covering map p: X^~ → X is a homeomorphism if and only if it is a bijection.) that p: X˜ → X is a homeomorphism, as required.

Let p: X˜ → X be a covering map over some topological space X, and let x₀ be some chosen basepoint of X. We shall investigate the dependence of the subgroup p_#(π₁(X˜, x˜)) of π₁(X, x₀) on the choice of the point x˜ in X˜,  where x˜ is chosen such that p(x˜) = x₀. We first introduce some concepts from group theory.

Let G be a group, and let H be a subgroup of G. Given any g ∈ G, let gHg⁻¹ denote the subset of G defined by

gHg⁻¹ = {g₀ ∈ G : g₀ = ghg⁻¹ for some h ∈ H}.

It is easy to verify that gHg⁻¹ is a subgroup of G.

Definition Let G be a group, and let H and H0 be subgroups of G. We say that H and H₀ are conjugate if and only if there exists some g ∈ G for which H₀ = gHg⁻¹ Note that if                    H₀ = gHg⁻¹      then  H = g⁻¹H₀g. The relation of conjugacy is an equivalence relation on the set of all subgroups of the group G. Moreover conjugate subgroups of G are isomorphic, since the homomorphism sending h ∈ H to ghg⁻¹ is an isomorphism from H to gHg⁻¹ whose inverse is the homorphism sending h 0 ∈ gHg⁻¹ to g⁻¹h₀g.

A subgroup H of a group G is said to be a normal subgroup of G if ghg⁻¹ ∈ H for all h ∈ H and g ∈ G. If H is a normal subgroup of G then gHg⁻¹ ⊂ H for all g ∈ G. But then g⁻¹Hg ⊂ H and H = g(g⁻¹Hg)g⁻¹ for all g ∈ G, and therefore H ⊂ gHg⁻¹ for all g ∈ G. It follows from this that a subgroup H of G is a normal subgroup if and only if gHg⁻¹ = H for all g ∈ G. Thus a subgroup H of G is a normal subgroup if and only if there is no other subgroup of G conjugate to H.

Lemma 1.7 Let p: X˜ → X be a covering map over a topological space X.

Let x₀ be a point of X, and let w₀ and w₁ be points of X˜ for which p(w₀) = x₀ = p(w₁). Let H₀ and H₁ be the subgroups of π₁(X, x₀) defined by

H₀ = p_#(π₁(X, w˜₀)), H₁ = p_#(π₁(X, w˜1)).

Suppose that the covering space X˜ is path-connected. Then the subgroups H₀ and H₁ of π₁(X, x₀) are conjugate. Moreover if H is any subgroup of π₁(X, x₀) which is conjugate to H0 then there exists an element w of X˜ for which p(w) = x and p_#(π₁(X, w˜ )) = H.

Proof Let α: [0, 1] → X˜ be a path in X˜ for which α(0) = w₀ and α(1) = w₁. (Such a path exists since X˜ is path-connected.) Then each loop σ in X˜ based at w₁ determines a corresponding loop α.σ.α⁻¹ in X˜ based at w0, where

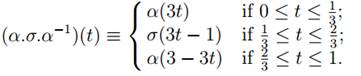
(This loop traverses the path α from w0 to w1, then continues round the loop σ, and traverses the path α in the reverse direction in order to return from w₁ to w₀.) Let                  η: [0, 1] → X be the loop in X based at the point x₀ given by η = p ◦ α, and let ϕ: π₁(X, x₀) → π₁(X, x₀) be the automorphism of the group π₁(X, x₀) defined such that ϕ([γ]) = [η][γ][η] ⁻¹ for all loops γ in X based at the point x₀. Then p ◦ (α.σ.α⁻¹) = η.(p ◦ σ).η⁻¹, and therefore p_#([α.σ.α⁻¹]) = [η]p_#([σ])[η]⁻¹ = ϕ(p_#([σ])) in π₁(X, x₀). It follows that ϕ(H₁) ⊂ H₀. Similarly ϕ⁻¹ (H₀) ⊂ H₁, where ϕ⁻¹ ([γ]) = [η]⁻¹ [γ][η] for all loops γ in X based at the point x₀. It follows that ϕ(H₁) = H₀, and thus the subgroups H₀ and H₁ are conjugate Now let H be a subgroup of π₁(X, x₀) which is conjugate to H₀. Then H₀ = [η]H[η]⁻¹ for some loop η in X based at the point x₀. It follows from the Path Lifting Theorem for covering maps (Theorem (Path Lifting Theorem)  that there exists a path α: [0, 1] → X˜ in X˜ for which α(0) = w₀ and p ◦ α = η. Let w = α(1).

Then p_#(π₁(X, w˜ )) = [η]⁻¹H₀[η] = H,  as required.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

Triple Torus

Thurston Elliptization Conjecture

Thurston,s Geometrization Conjecture

Real Projective Plane

Pseudometric Topology

Pseudocrosscap

Parallelizable

Möbius Strip

Möbius Shorts

Path

Product Topology

Handle