Theorem 1.6 π₁(S¹, b) ≅Z for any b ∈ S¹.

Proof We regard S₁ as the unit circle in R². Without loss of generality, we can take b = (1, 0). Now the map p: R → S¹ which sends t ∈ R to (cos 2πt,sin 2πt) is a covering map, and b = p(0). Moreover p(t₁) = p(t₂) if and only if t₁ − t₂ is an integer; in particular p(t) = b if and only if t is an integer.

Let α and β be loops in S¹ based at b, and let ˜α and β˜ be paths in R that satisfy p ◦ α˜ = α and p ◦ β˜ = β. Suppose that α and β represent the same element of π₁(S¹, b). Then there exists a homotopy F: [0, 1] × [0, 1] → S₁

such that F(t, 0) = α(t) and F(t, 1) = β(t) for all t ∈ [0, 1], and F(0, τ ) = F(1, τ ) = b for all τ ∈ [0, 1]. It follows from the Monodromy Theorem  (Theorem 1.5) that this homotopy lifts to a continuous map G: [0, 1]×[0, 1] → R satisfying p ◦ G = F. Moreover G(0, τ ) and G(1, τ ) are integers for all τ ∈ [0, 1], since p(G(0, τ )) = b = p(G(1, τ )). Also G(t, 0)−α˜(t) and   G(t, 1)− β˜(t) are integers for all t ∈ [0, 1], since p(G(t, 0)) = α(t) = p(α˜ (t)) and p(G(t, 1)) = β(t) = p(β˜(t)). Now any continuous integer-valued function on [0, 1] is constant, by the Intermediate Value Theorem. In particular the functions sending τ ∈ [0, 1] to G(0, τ ) and G(1, τ ) are constant, as are the functions sending t ∈ [0, 1] to G(t, 0) − α˜(t) and G(t, 1) − β˜(t). Thus

G(0, 0) = G(0, 1),                     G(1, 0) = G(1, 1),  

G(1, 0) − α˜(1) = G(0, 0) − α˜(0),                 G(1, 1) − β˜(1) = G(0, 1) − β˜(0).

On combining these results, we see that

α˜(1) − α˜(0) = G(1, 0) − G(0, 0) = G(1, 1) − G(0, 1) = β˜(1) − β˜(0)

We conclude from this that there exists a well-defined function λ: π₁(S¹, b) → Z characterized by the property that λ([α]) = α˜ (1)−α˜(0) for all loops α based at b, where                   α˜: [0, 1] → R is any path in R satisfying p ◦ α˜ = α.

Next we show that λ is a homomorphism. Let α and β be any loops based at b, and let α˜ and β˜ be lifts of α and β. The element [α][β] of π₁(S¹, b) is represented by the product path α.β, where

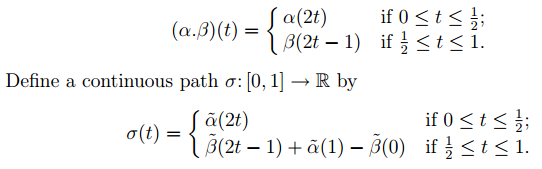
(Note that σ(t) is well-defined when t =1/2.) Then p ◦ σ = α.β and thus

 λ([α][β]) = λ([α.β]) = σ(1) − σ(0) = α˜ (1) − α˜(0) + β˜(1) − β˜(0)

                 = λ([α]) + λ([β]).

Thus λ: π₁(S¹, b) → Z is a homomorphism.

Now suppose that λ([α]) = λ([β]). Let F: [0, 1] × [0, 1] → S¹ be the homotopy between α and β defined by

              F(t, τ ) = p( (1 − τ ) α˜ (t) + τβ˜(t) ),

where α˜ and β˜ are the lifts of α and β respectively starting at 0. Now β˜(1) = λ([β]) = λ([α]) = α˜ (1), and β˜(0) = α˜ (0) = 0. Therefore F(0, τ ) = b = p(α˜ (1)) = F(1, τ ) for all              τ ∈ [0, 1]. Thus α ≃β rel {0, 1}, and therefore  [α] = [β]. This shows that λ: π₁(S¹, b) → Z is injective.

The homomorphism λ is surjective, since n = λ([γ_n]) for all n ∈ Z, where the loop γ_n: [0, 1] → S¹ is given by γ_n(t) = p(n_t) = (cos 2πnt,sin 2πnt) for all t ∈ [0, 1]. We conclude that                   λ: π₁(S¹ , b) → Z is an isomorphism.

We now show that every continuous map from the closed disk D to itself has at least one fixed point. This is the two-dimensional version of the Brouwer Fixed Point Theorem.

Theorem 1.7 Let f: D → D be a continuous map which maps the closed disk D into itself. Then f(x₀) = x₀ for some x₀ ∈ D Proof Let ∂D denote the boundary circle of D. The inclusion map i: ∂D → D induces a corresponding homomorphism  i_#: π₁(∂D, b) → π₁(D, b)of fun damental groups for any b ∈∂D.

Suppose that it were the case that the map f has no fixed point in D.

Then one could define a continuous map r: D → ∂D as follows: for each x ∈ D, let r(x) be the point on the boundary ∂D of D obtained by continuing the line segment joining f(x) to x beyond x until it intersects ∂D at the point r(x). Note that r|∂D is the identity map of ∂D.

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة مناحل الكفيل تختتم مشاركتها في معرض السليمانية الدولي للزراعة والصناعات الغذائية

لتوثيق التراث العلمي.. وفد قسم شؤون المعارف يلتقي عددًا من أعلام مدينة النجف

قسم الشؤون الفكرية ومؤسسة الشهداء يبحثان سبل تعزيز التعاون في برامج الذاكرة الوطنية

المجمع العلمي يقيم دورته التطويرية الثالثة لإعداد أساتذة الدورات الصيفية في صلاح الدين

المزيد

الآخبار الصحية

طبيب يكشف تأثير برودة الشتاء على النوم

دون أن تعلم.. 10 عادات يومية تسرع شيخوخة جسمك

تقرير: النيكوتين خطر على القلب مهما كانت الطريقة

أيهما أفضل لصحتك.. زبدة الفول السوداني أم النوتيلا؟

المزيد

الآخبار التكنلوجية

السعودية تدشن أكبر نظام لتخزين الكهرباء بالبطاريات في العالم !

بأمر تنفيذي.. ترامب يؤكد هدف عودة الأميركيين إلى القمر في عام 2028

بعيدا عن البشر.. "قتال جوي في الفضاء" بين أميركا والصين

كشف مذهل في قاع "برمودا" !

المزيد

مواضيع ذات صلة

Triple Torus

Thurston Elliptization Conjecture

Thurston,s Geometrization Conjecture

Real Projective Plane

Pseudometric Topology

Pseudocrosscap

Parallelizable

Möbius Strip

Möbius Shorts

Path

Product Topology

Handle