


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 20-12-2015
Date: 23-12-2015
Date: 8-2-2017
|
Oppenheimer–Snyder collapse
Scenario and model
The Oppenheimer-Snyder model [11] describing the inevitable collapse of a ball of dust to a black hole is an exact solution of the general-relativistic field equations of gravitation. Rigorous solutions like this one are very important for deeper insight into the four-dimensional spacetime structure and enable us to ask correct physical questions in the context of general relativity. The point made here is to understand the formation of a black hole from ‘normal’ matter. Of course, dust is not very realistic in view of the complex structure of real collapsing stars.
Let us now model the main stages of a collapse:
(i) Stationary phase before the collapse: the star could be thought to be a static spherically symmetric perfect fluid ball with the energy-momentum tensor
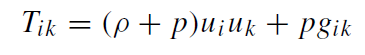 (1.1)
(1.1)
where ρ, p, ui, and gik are the mass density, the pressure, the four-velocity of the mass elements, and the metric respectively. (Units are chosen such that G = c = 1.) One could, e.g., think of the (interior and exterior) Schwarzschild solution).
(ii) End of nuclear burning and start of the collapse: all of a sudden, the pressure p breaks down (p = 0). For a moment, the resulting ball of dust (p = 0) with
 (1.2)
(1.2)
remains at rest.
(iii) Phase of collapse: since there is no pressure to balance gravity, the ball (star) begins to shrink. For dust, we expect an inevitable collapse and, finally, the formation of a black hole.
Solution of the field equations
1.1 The problem
To obtain the spacetime line element
 (1.1)
(1.1)
for the collapsing ball of dust, we have to integrate the Einstein equations
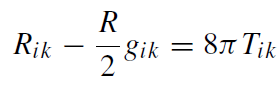 (1.2)
(1.2)
where
 (1.3)
(1.3)
The solution must be asymptotically flat (gik → ηik at infinity, the ‘boundary value problem’) and regular everywhere for all times t ≥ 0. According to our model, the star should be at rest for t = 0 (the ‘initial value problem’). To solve the boundary/initial value problem, we will solve the interior and exterior field equations separately and match the interior to the exterior part afterwards (‘matching problem’). The procedure relies heavily on spherical symmetry.
1.2 Exterior solution
An aid to the understanding of the following material can be gained by reading the appropriate passages of the excellent book from Misner, Thorne and Wheeler [12] (known as MTW).
Spherical symmetry means that ds2 is form invariant under the group of spatial orthogonal transformations and can therefore be put in the form
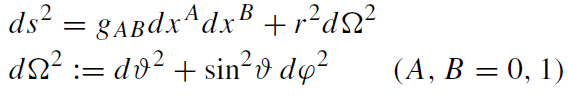 (1.4)
(1.4)
where (gAB) and r are functions of x0 and x1 alone,
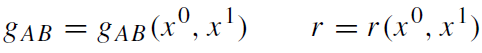 (1.5)
(1.5)
and x2 = ϑ(0 ≤ ϑ ≤ π) and x3 = ϕ(0 ≤ ϕ ≤ 2π) are the usual spherical coordinates.
The line element (1.4) may further be reduced by a suitable choice of the coordinates (x0, x1). The following three examples are useful for collapse discussions:
(i) Schwarzschild coordinates:
 (1.6)
(1.6)
This form may be obtained by a coordinate transformation r = r (x0, x1), t = (x0, x1). The vacuum equations (1.2), (1.3),
Rik = 0 (1.7)
give ∂λ/∂t = 0, ∂2ν/∂t2 = 0, first of all, and after a time scaling of the form t' = t' (t) the exterior Schwarzschild solution
 (1.8)
(1.8)
where M is the reduced mass of the star. (Note that we have put G = 1, c = 1.
Hence we do not distinguish between the mass M measured in kilograms and the reduced mass MG/c2 expressed in metres.) Obviously, the only vacuum solution with spherical symmetry is the exterior Schwarzschild solution (Birkhoff's theorem, 1923) and that solution is static. As a consequence, a collapsing spherically symmetric star cannot emit gravitational waves. The Schwarzschild metric (1.8) is regular for r > 2M and has, apparently, a singularity at the Schwarzschild radius r = 2M. However, the geometry (the curvature tensor) is regular there. Thus, ‘better’ coordinates in the domain r ≤ 2M must exist.
(ii) Kruskal–Szekeres coordinates:
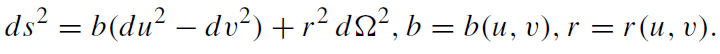 (1.9)
(1.9)
Any two-metric (such as gAB in (1.4)) is conformally equivalent to a flat two metric. We have put x0 = u, x1 = v. Inserting (1.9) into the field equations (1.7), we obtain b = b(u, v) and r = r (u, v),
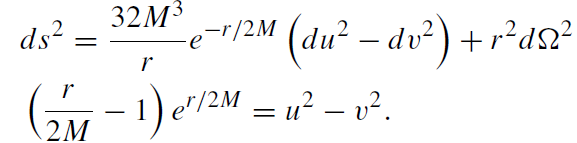 (1.10)
(1.10)
The Kruskal–Szekeres coordinates (u, v) are related to the Schwarzschild coordinates by
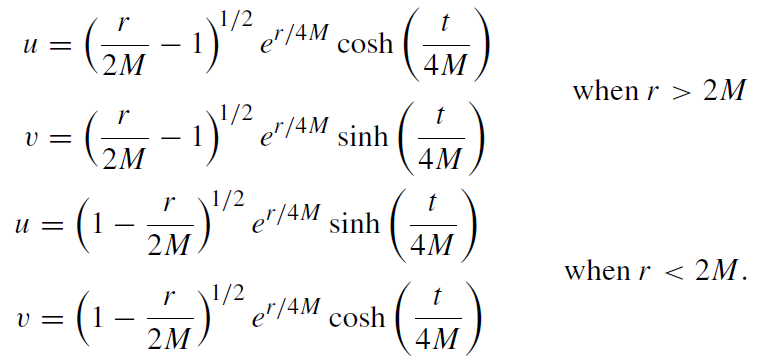 (1.11)
(1.11)
There is no coordinate singularity at r = 2M. Kruskal–Szekeres coordinates are well suited for the global analysis of black holes.
(iii) Ingoing Eddington–Finkelstein coordinates:
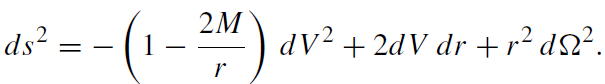 (1.12)
(1.12)
This line element can be obtained from (3.8) by the coordinate transformation
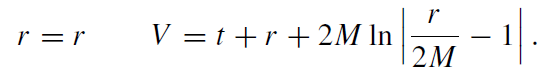 (1.13)
(1.13)
The coordinates are adapted to ingoing light rays V = constant, cf MTW [12].
1.3 Interior solution
The field equations (1.2) together with the dust matter model (1.3) imply local mass conservation
(ρui );i = 0 (1.14)
and geodesic motion of the mass elements,
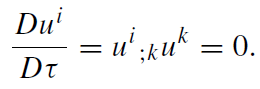 (1.15)
(1.15)
Equations (1.14) and (3.15) are a direct consequence of the local energy momentum conservation,
T ik; k = 0.
To get a manageable model, we are on the look-out for further hydrodynamic simplifications. Because of the radial motion of the mass elements, the vorticity of the four-velocity has to vanish. Let us assume, in addition, that the motion be shear free. Then we arrive at [13],
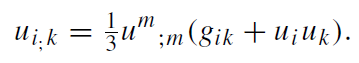 (1.16)
(1.16)
(Note that (3.18) implies ui,k- uk,i = 0 whence Dui /Dτ = 0.) We may now choose the world lines of the mass elements to be the time lines (‘comoving coordinates’),
(ui ) = (1, 0, 0, 0). (1.17)
Then, by means of (1.16), the line element (1.1) can be put in the following form
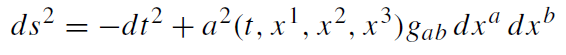 (1.18)
(1.18)
where gab does not depend on t.
As a consequence of the field equations (1.2) for dust (1.3), the subspace t = constant has a constant (vanishing, positive or negative) curvature. Introducing spherical coordinates χ (0 ≤ χ < χ0), ϑ (0 ≤ ϑ ≤ π), ϕ (0 ≤ ϕ ≤ 2π), the line element (1.18) takes the form
 (1.19)
(1.19)
where f characterizes the three curvature types. The remaining field equations (and their consequence (3.14)) reduce to the simple first-order system
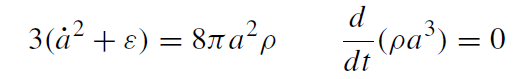 (1.20)
(1.20)
where ε = (0, 1,−1) corresponds to the three values of f , and a dot denotes time derivative.
The line element (1.19) describes the interior geometry of an expanding ( ˙a > 0) or contracting ( ˙a < 0) dust ball. Its three-surface χ = χ0 is the interface to the exterior Schwarzschild region. Interestingly, our initial value problem (‘star at rest’),
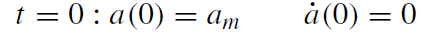 (1.21)
(1.21)
singles out positive curvature,
ε = 1. (1.22)
(ε = 0,−1 is not compatible with ˙a(0) = 0 in (1.20).) Then the solution of (1.20)-(1.22) is given by
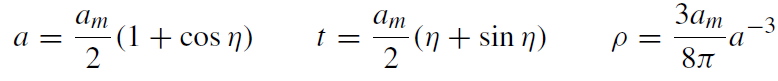 (1.23)
(1.23)
where
0 ≤ η ≤ π.
The equations (1.23) describe a dust ball whose scale factor a(t) shrinks from the initial value a = am(η = 0, t = 0) to zero (η = π, t = πam/2).
The dust model has a fundamental meaning for cosmology: the equations (1.19), (1.20) describe the geometry and mass distribution of an open (ε = 0,−1) or closed (ε = 1) Friedman universe.
We have now to match the interior (Friedman) (1.19), (1.23) and the exterior (Schwarzschild) solution.
1.4 Matching of geometries
The interface between the interior and exterior geometry is formed by the geodesic (world) lines of the mass elements on the surface of the dust ball. This ‘world tube’ can be described in the interior as well as in the exterior coordinates. In interior coordinates, the radial surface geodesics are characterized by the equation x0 = τ (cf (1.17), dx0/dτ = 1) and constant values of ϑ, ϕ, χ for all proper times τ ≥ 0,
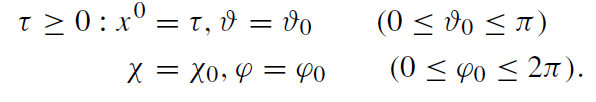 (1.24)
(1.24)
However, the same world lines have to be radial geodesics of the exterior Schwarzschild solution (1.8). Integrating the underlying equation
 (1.25)
(1.25)
for the initial values
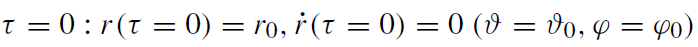 (1.26)
(1.26)
we obtain
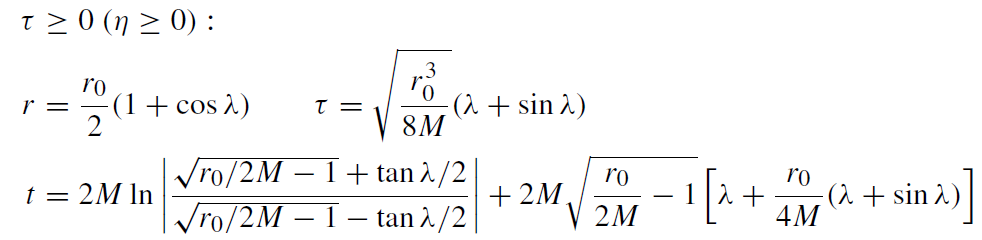 (1.27)
(1.27)
where the real parameter λ is restricted by
0 ≤ λ ≤ π. (1.28)
Obviously, τ = 0 corresponds to the parameter value η = 0.
The identification of the equations (1.24) and (1.27) requires coordinate-free criteria. It can easily be seen that the proper time τ ,
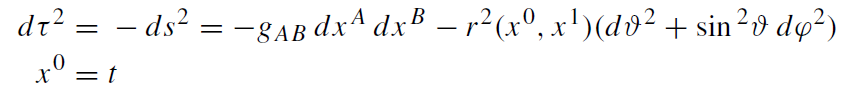 (1.29)
(1.29)
and the circumference C(τ ) of the three-dimensional interface (‘world tube’) along the slice S : x A = constant (A = 0, 1), ϑ = π/2
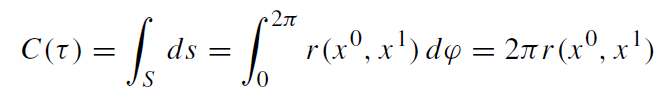 (1.30)
(1.30)
have an invariant geometrical meaning. Making use of the equations (1.19), (1.23), and (1.24), we obtain in interior coordinates
 (1.31)
(1.31)
whereas, according to (1.27), the calculation in exterior coordinates yields
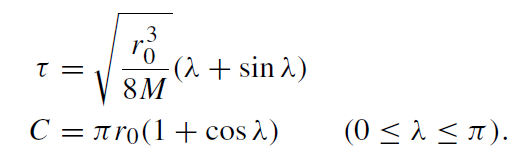 (1.32)
(1.32)
From the identification of the equations (1.31) and (1.32) we have
 (1.33)
(1.33)
Thus the ‘interior’ constants am and χ0, describing the maximum extension of the star (a = am) and its surface (χ = χ0), can be expressed in terms of the star's total mass M and its maximum ‘radius’ r0.
It can be shown that the (necessary) conditions (1.33) are sufficient to glue together smoothly the pieces of Friedman geometry describing the star’s interior,
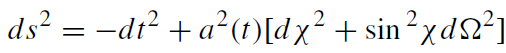 (1.34)
(1.34)
a(t) as in (1.23) 0 ≤ χ ≤ χ0.
and Schwarzschild geometry describing its exterior,
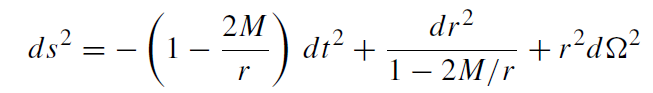 (1.35)
(1.35)
r (t) ≤ r < ∞ r (t) as in (1.27).
Both pieces of geometry glued together smoothly along the interface form only one solution to the Einstein equations. It describes a collapsing model star whose circumference shrinks permanently from C = 2πr0 (λ = 0, ‘star at rest start of collapse’) to C = 0 (λ = π, ‘end of collapse’).
Physical interpretation
There is no obvious geometrical singularity during the collapse, not even when a mass point of the star's surface reaches the ‘dangerous’ coordinate value r = 2M.
And to introduce ‘better’ exterior coordinates, as, e.g., Kruskal– Szekeres or Eddington–Finkelstein coordinates.
To obtain the world line of a surface point of the star in Eddington– Finkelstein coordinates,
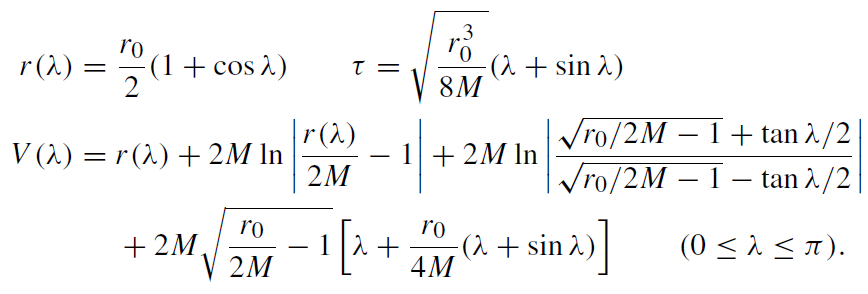 (1.1)
(1.1)
The diagram shown in figure 4 was taken from MTW [12, p 849]. It uses slightly modified Eddington–Finkelstein coordinates
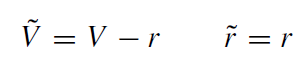 (1.2)
(1.2)
and illustrates the collapse of a star whose radius r drops from r0 = 10M to r = 0. According to (1.1), the proper time interval Δτ of the collapse, as measured by a comoving observer placed on the star's surface, is surprisingly short
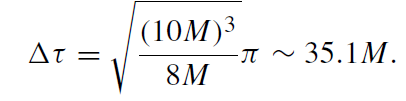 (1.3)
(1.3)
Even the critical radius r = 2M is reached in a similarly short proper time of Δτ = 33.7M. Since, as we will see, this event marks the birth of a black hole, an external observer placed at fixed spatial coordinate values (at r = 10M in figure 1.1) could ask him- or herself after a while whether the black hole had
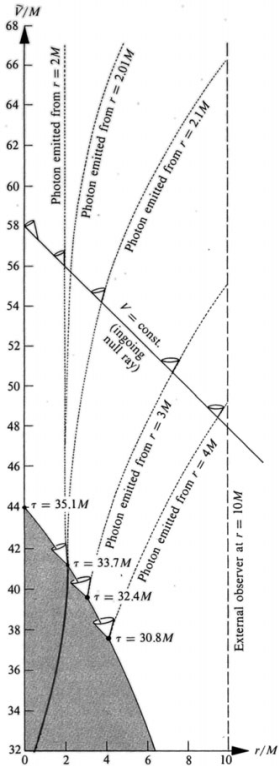
Figure 1.1. Oppenheimer–Snyder collapse in modified Eddington–Finkelstein coordinates (adapted from MTW [12]). The diagram depicts a series of photons emitted radially from the surface of the collapsing star and received by an observer at r = r0 = 10M. Any photon emitted radially at the Schwarzschild radius r = 2M stays at r = 2M forever. This external event horizon is the continuation of the internal event horizon (full curve in the shaded interior region of the star).
already formed or not. The scenario sketched in figure 1.1 demonstrates that such a question is ill posed. To communicate with each other, the comoving observer and the external observer could exchange light signals (photons). Since the Eddington-Finkelstein are adapted to radial ingoing light rays (V, ϑ, ϕ : constants, ds2 = 0), the world line of an ingoing photon in the modified coordinates (1.2) is given by
 (1.4)
(1.4)
All ingoing null rays are parallel to the one sketched in figure 1.1, i.e. all photons emitted from the external observer reach the domain r = 0. We get for the outgoing light rays describing photons emitted from the surface of the collapsing star
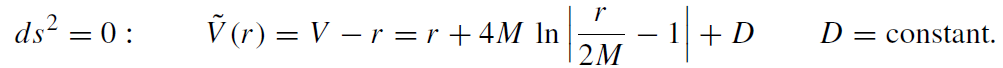 (1.5)
(1.5)
One may fix the constant D = D(η) from the intersection with the star's surface (1.1). Figure 1.1 depicts a series of such photon world lines emitted from the surface of the collapsing star and received by the observer at r = 10M. It illustrates the way in which the external observer distinguishes the collapse. Consider a series of uniformly spaced light signals emitted by the comoving observer. Received at the external observer, they would become more and more widely spaced. Finally, any photon emitted at r = 2M stays at r = 2M forever and can never reach the external observer. For this reason, the domain r = 2M is called the event horizon. In the diagram it is marked by the world line of the photon emitted from r = 2M. After the Schwarzschild radius r = 2M has been passed, the external observer never receives a signal: all photons emitted from the star's surface are sucked into the singularity at r = 0, which is a real singularity of spacetime geometry.
Let us now return to the question of black hole formation. From the point of view of the external observer, the star never gets beyond its Schwarzschild radius r = 2M. This seems to contradict the observation of the comoving observer that the star rapidly reaches r = 2M and r = 0. A physicist, who applies Einstein's theory, must not identify his or her position with that of the external or the comoving observer. The physicist knows the geometry of the four-dimensional spacetime, the world lines of matter and observers, and the physical processes in spacetime. He can visualize this knowledge by four-dimensional diagrams such as that in figure 1.1. This complete information enables him/her to formulate and answer ‘reasonable’ (i.e. physical) questions. From his or her four-dimensional point of view, the event ‘star surface passes the Schwarzschild radius r = 2M’ marks the formation of a black hole characterized by its event horizon. He or she
knows that processes of the black hole's history, such as the emission of photons from the star's surface, can influence the remotest future of an external observer. The four-dimensional view of the gravitational phenomena connected with the black hole formation requires the analysis of the internal geometry of the black hole and the processes inside the black holes, too. The internal part of spacetime cannot be ignored with the argument that the external observers (as we are) will never obtain information from the interior.
The Eddington–Finkelstein coordinates are adapted to the vacuum domain outside the star. To depict the world lines of the mass elements or to extend the event horizon to the interior of the star (gray domain in figure 1.1), one needs ‘internal’ Eddington–Finkelstein coordinates. The extension is not unique. Radially ingoing light rays V = constant and the radial coordinate r = a(t) sin χ.
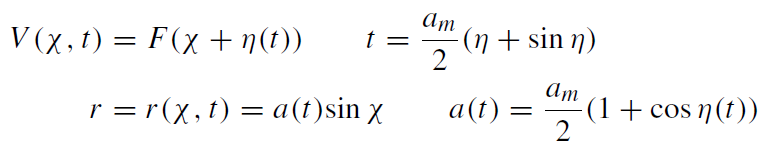 (1.6)
(1.6)
where F is an arbitrary function of χ + η. F can be fixed by the identification of the internal ingoing light rays V = F(χ + η) = constant with the external light rays V = constant along the surface.
The horizon inside the star consists of those outgoing geodesic lines that meet the external event horizon at the star's surface χ = χ0,
 (1.7)
(1.7)
In figure 1.1, the internal event horizon is depicted by the full line inside the star.
All internal ingoing light rays ‘beneath’ that line arrive at the surface before the black hole has passed through its Schwarzschild radius r = 2M and can therefore escape to infinity. The light rays beyond the line arrive at the surface inside the black hole and get pulled into the singularity at r = 0.
Unfortunately, there is not enough space for a detailed discussion of further effects in this chapter. Following the textbook of MTW [12], I confine myself to a description of some interesting results.
Light propagation. Light emitted from the collapsing star becomes more and more redshifted and reaches a relative redshift limit of z  2 at a distant external observer. The total luminosity decays exponentially in time. Light from the star in its late stages (before the black hole transition) is not dominated by ‘radial photons’ but by photons that were deposited by the star in (unstable) circular orbits as its surface passed through r = 3M.
2 at a distant external observer. The total luminosity decays exponentially in time. Light from the star in its late stages (before the black hole transition) is not dominated by ‘radial photons’ but by photons that were deposited by the star in (unstable) circular orbits as its surface passed through r = 3M.
Fate of the star beyond its horizon. The star and the entire internal geometry collapse inevitably in a spacetime singularity which crushes the collapsing matter to infinite density.
Fate of the comoving observer. There are no special problems at r = 2M (imagine the ‘soft’ formation of a huge galactic black hole of 106 solar masses!) Eventually, the observer crushes to zero volume and indefinitely extended length at r = 0.
The Tolman–Oppenheimer model has been generalized for other dust balls [14, 15] and different energy–momentum tensors [16]. Special attention is being paid to the non-spherical collapse as a source of gravitational radiation. There is justified hope that gravitational waves emitted from type IIa supernovae and other collapsing cosmic sources could be detected with the aid of the laser interferometers of the VIRGO, LIGO, or GEO 600 projects.
Most insiders are convinced that the end product of a non-spherical collapse with non-vanishing angular momentum is a rotating black hole whose external geometry is described by the stationary and axially symmetric Kerr solution (see Hawking and Ellis [17] for a review) which, in turn, is determined uniquely by the parameters of mass and angular momentum. It would be highly desirable to elaborate more precisely on such an assertion. Before that, the question remains undecided as to whether cosmic collapse processes lead inevitably to the formation of black holes. Another very important problem is the question whether the singularity at the end point of spherical collapse is typical for all collapse processes or whether it can be removed in more general collapses. Such questions were first analyzed by Penrose [18] and Hawking and Penrose [19]. For an introduction to the analysis of singularities one should study the book of Hawking and Ellis [17].



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|