Special relativity and Newton’s theory: a clash

Apparently, the space surrounding us has three dimensions. Together with the one-dimensional time, it constitutes four-dimensional (4D) spacetime. Distinguished frames of reference are the inertial frames. They are understood as infinitely extended frames in which force-free particles are at rest or move uniformly along straight lines in the sense of Euclidean geometry. In them, we may introduce coordinates

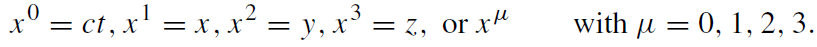 (1.1)

As a rule, all Greek indices shall run from 0 to 3. In an empty space with respect to an inertial frame of reference, there is no distinction between the different points in it and no preferred direction. Likewise, there is no preferred instant of time.

With this homogeneous and spatially isotropic spacetime in mind, we state the special relativity principle: the laws of physics are the same in all inertial frames.

A prototypical law of nature to be stated in this context is the principle of the constancy of the speed of light: light signals in vacuum are propagated rectilinearly, with the same speed c at all times, in all directions, in all inertial frames, independently of the motion of their sources.

By means of these two principles, we can deduce the Poincar´e (or inhomogeneous Lorentz) transformations which encompass four spacetime translations, three spatial rotations, and three Lorentz boosts, i.e. velocity transformations. The ‘essence’ of this transformation can also be expressed in a somewhat different manner.

We define a tensor T of covariant rank k and contravariant rank l, respectively, by means of its behavior under coordinate transformations,

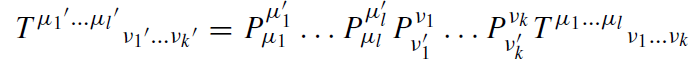 (1.2)

where we have introduced the Jacobian matrix and its inverse according to

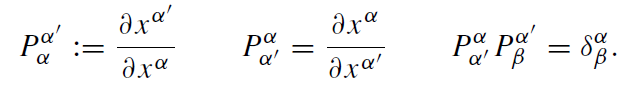 (1.3)

The summation convention is assumed, i.e. summation is understood over repeated indices. The values of the components of tensors do change, but only in the specific linear and homogeneous manner indicated here. Equations of tensors remain form invariant or covariant, i.e. the transformed equations look the same but with the unprimed indices replaced by primed ones. If one contracts co and contravariant tensors in such a way that no free index is left, v_iwⁱ , e.g. one gets a scalar, which is invariant under transformations, i.e. it does not change its value. The latter represents an observable quantity. The generic case of a covariant tensor of first rank is the partial derivative of a scalar function φ,_α := ∂φ/∂x^α and the typical contravariant tensor is the coordinate differential dx^α. Besides tensors, we also need spinors in special relativity, but they are not essential in gravitational theory.

We define the Minkowski metric as follows.

 (1.4)

where (in Cartesian coordinates)

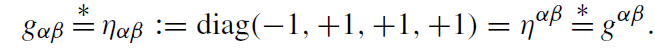 (1.5)

The g_αβ denote the inverse of the metric tensor. Under a Poincar'e transformation, the components of the Minkowski metric η_αβ remain numerically invariant. This metric defines an invariant spatiotemporal distance between two spacetime points or events, as they are called. Spatial distance alone between two points can be different for different observers and the same applies to time intervals. This manifests itself in the well-known effects of time dilation and length contraction.

Now we are able to express the principle of special relativity in the following way: the equations of physics describing laws of nature transform covariantly under Poincar'e transformations.

How can we apply this to gravity? In Newtonian gravity, the potential obeys the Poisson equation Δφ = 4πGρ. The corresponding wave equation can be represented as

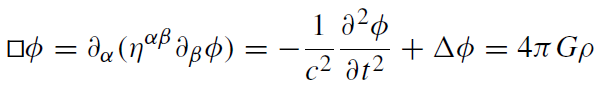 (1.6)

and thus is manifestly Poincar'e invariant. Hence, the Poisson equation as such is not Poincar'e invariant but only a limiting case of the wave equation for static situations.

The first idea for a Poincar'e covariant equation for the gravitational potential would be the obvious generalization by admitting the gravitational potential φ and the source ρ to be time dependent and interrelating both by means of a gravitational wave equation □φ = 4πGρ. But what is the source ρ now? In the case of a pressure-less fluid or a swarm of dust particles where all components move parallelly with the same velocity (and correspondingly have a common rest system), a Poincar'e invariant meaning for the mass density can be found, but this is not possible in general. Moreover, we learn from special relativity that mass and energy are equivalent. Binding forces and therewith stress within matter are expected to contribute to its gravitating mass. Thus, in a relativistic theory of gravitation, we have to replace mass density by energy density. Next, we have to look for a Poincar'e invariant quantity which contains the (mass-)energy density and will reduce to it in special cases.

And indeed, special relativity provides such a quantity. In electrodynamics, Minkowski found a symmetric second-rank tensor T ^αβ_Max whose divergence yields the Lorentz force density ∂αT ^αβ _Max = f ^β. For an electrically charged perfect fluid, characterized by mass-energy density ρ and pressure p, the equations of motion can be written in the form

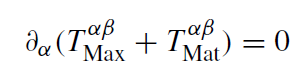 (1.7)

where we have introduced the energy momentum tensor of the perfect fluid:

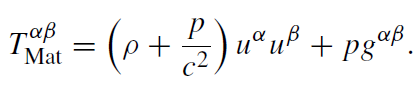 (1.8)

The vector uα = dx^α/dτ = γ (v)(c, v) is the four-velocity of the fluid elements (and v the three-velocity with respect to the chosen frame of reference. The Lorentz factor γ is given by γ (v) := (1 − v²/c²)^−1/2). The components of the energy momentum tensor are not invariant, of course. In the rest frame of the fluid, the observer sees a fluid at rest with a certain mass-energy distribution and an isotropic pressure p: T ^αβ= diag (ρc², p, p, p). However, with respect to a moving frame, there is a moving energy distribution which results in an energy flux density. Moreover, isotropic pressure transforms into anisotropic stress etc. In general, we arrive at the following structure (momentum flux density and stress are equivalent notions, i, j = 1, 2, 3):

 (1.9)

Now we can construct a scalar invariant encompassing the mass-energy density in the following way:

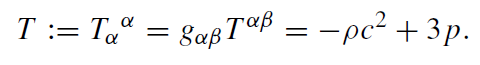 (1.10)

For 'non-relativistic matter', we find ρ << 3 p/c². Thus, indeed, T ≈ ρc². The Poincar'e-invariant field equation

 (1.11)

then yields the Newtonian Poisson equation in an appropriate limiting case and for an appropriately chosen coupling constant κ.

At first sight, this defines a viable gravitational theory. However, it turns out that this theory runs into serious conflicts with observations. A scalar gravitational theory does not allow for the deflection of light in gravitational fields because a scalar field cannot be coupled reasonably to the electromagnetic field, since the electromagnetic energy–momentum tensor is traceless. Light deflection has been experimentally confirmed beyond doubt. Thus, we have to look for different possibilities in order to interrelate electromagnetic energy–momentum and the gravitational potential. To this end we will now turn to the gravitational field.

Not only have we no direct intuition of the equality of two periods, but we have not even direct intuition of the simultaneity of two events occurring in two different places.

                                                                                           Henri Poincar'e (1902)