مبدأ اللايقين

منذ اكتشاف الطبيعة الموجية للإلكترون والتجارب العديدة تتوالى للنظر فيما إذا كانت هناك جسيمات أخرى تسلك نفس السلوك. ودراسة الجسيمات ذات الأبعاد الذرية أو ما دون الذرية سهلة نسبياً فيما يتعلق بالظواهر الموجية، ولم يكتشف أي استثناء لمعادلة دي برولي للأطوال الموجية. والواقع أن استعمال الإلكترونات والنيوترونات إلى جانب أشعة إكس في تجارب الحيود التي صممت لدراسة التركيب البلوري، قد أصبح من الامور الشائعة.

تؤدي الطبيعة الموجية لجميع الجسيمات إلى مبدأ فلسفي عظيم . فقد كان الجدل قائماً بين الفلاسفة قبل هذا الاكتشاف، حول ما إذا كان مصير الكون محدداً تماماً أم لا.

          هل نستطيع ــ ولو من حيث المبدأ ــ أن نحدد موقع وسرعة وطاقة جميع الجسيمات في الكون ثم أن نتنبأ بمجرد الأحداث المستقبلية ؟ يبدو أن الطبيعة الموجية لجميع الجسيمات تتطلب منا أن نجيب بالنفي على هذا السؤال. والواقع أن هذه الحقيقة كامنة في مبدأ اللايقين لهاينزنبرك.

دعنا ننظر في البداية في كيفية تحديد موقع جسيم ما بأقصى قدر من الدقة، فلكي نحدد الموقع لابد أن نجعل جسيماً ثانياً على الأقل (سنسميه الجسيم المجس) يصطدم مع  الجسيم المستهدف، ثم نسجل الزاوية التي يتطاير بها الجسيم المجس. ولكي نقلل قدر الإمكان من تأثير الجسيم المجس على موقع الجسيم المستهدف، فإننا سنستخدم فوتوناً منفرداً طوله الموجي λ ليقوم بدور المجس. يحمل هذا الفوتون كمية تحرك مقدارها p = h/λ وطاقة مقدارها E = hc/λ. وسنستخدم كاشفاً للجسيم (قد يكون عدسة مثلاً) يقابل زاوية مقدارها α عند الجسيم باتجاه المحور y. وعند تطاير الفوتون من على الجسيم فإنه ينقل بعضاً من كمية تحركه إلى الجسيم. وسيكتسب الفوتون خلال العملية بعضاً من المركبة x لكمية التحرك ، ولكن مركبة كمية التحرك هذه ستتخذ أقصى قيمة ممكن p_x = p sin αΔ حتى يتسنى للفوتون أن يدخل إلى العدسة ويكتشف هناك. وحيث أن كمية التحرك لابد وأن تكون محفوظة، فإن الهدف لابد أن يكتسب مركبة x من كمية التحرك مساوية ومضادة لتلك التي اكتسبها الفوتون. وكل ما يقال الآن، هو إنه لكي يتم اكتشاف الفوتون، فإن كمية تحرك الهدف ستكون لا يقينية بالمقدار

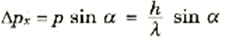
 أن ظواهر الحيود تحد من الدقة التي يمكن بها تحديد موقع مصدر نقطي. ويمكننا كتابة هذا الحد تقريباً على أنه x ≈ λ/sin αΔ، وعلى ذلك فإنه اكتشاف الفوتون كفيل بتحديد موقع الجسيم المستهدف في حدود هذا القدر من اللايقين في الموضع فحسب. فإذا قمنا الآن بضرب قيمتي اللايقين في الموضع وكمية التحرك بالنسبة للجسيم المستهدف، فإننا نحصل على :

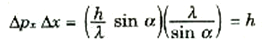
وبعبارة أخرى، فعندما نلجأ لأكثر التجارب دقة، يمكن تخليلها ، من اجل تحديد موضع جسيم، ونقيس في نفس الوقت كمية تحركه، فإن حاصل ضرب مقداري اللايقين الذاتي لهاتين الكميتين لابد ــ على الأقل ــ أن يكون مساوياً لثابت بلانك. ويتضح أن هذه علاقة عامة تماماً وهي إحدى صور مبدأ هاينزنبرك للايقين.

ومن الممكن الوصول إلى صورة أخرى لمبدأ اللايقين من خلال استدلال مشابه لهذا. إذا كان اللايقين في موضع الجسيم الهدف هو x ≈ λΔ ، فإن الزمن الذي يستغرقه الفوتون لكي يقطع هذه المسافة t = λ/cΔ وتتراوح كمية الطاقة التي يمكن للجسيم الهدف أن يستقبلها من الفوتون بين الصفر وحتى قيمة قصوى تساوي طاقة الفوتون كلها hc/λ ولذلك فإن الطاقة التي يحصل عليها الجسيم تتضمن مقداراً من اللايقين هو E = hc/λΔ ، فإذا ضربنا قيمتي اللايقين في الطاقة والزمن، نحصل على:

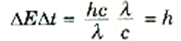
وهكذا أصبح لدينا علاقتان للايقين، إحداهما تتضمن كمية التحرك والأخرى تتضمن الطاقة ؛ وقد اقترحنا لأول مرة من فيرنر هاينزنبرك عام 1927. دعنا الآن نصوغ العلاقتين بصورة أكثر دقة. طبقاً لمبدأ اللايقين لهاينزنبرك فإن:

عند قياس الإحداثي x وكمية  التحرك p_x لجسيم ما في نفس اللحظة فإن،

(1)     

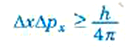
حيث xΔ وp_x Δ هما قيمتا اللايقين في x و p. وبالمثل، عند قياس الطاقة E لجسيم ما في لحظة t فإن قيمتي اللايقين EΔ وΔt ترتبطان بالعلاقة:

(2)         

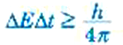
وسبب وضع العلامة ≤ إنه في حالة أية قياسات واقعية لا مفر من إثارة اضطراب للجسيم المستهدف بدرجة أكبر من التي يحدثها قياس فوتون واحد مثالي.

وهكذا نجد أنه من المستحيل، ولو من حيث المبدأ، أن نعرف كل شيء عن جسم ما إذا سيكون هناك دائماً قدر من اللايقين حول طاقته الحقيقية في لحظة معينة، وحول كمية تحركه الحقيقية في موقع معين. هذه إحدى النتائج الأساسية اللازمة لمفاهيم كمات الضوء والموجات الجسيمية. من الواضح، إذن،  إن هناك حاجة إلى صياغة جديدة لوصف الجسيمات الذرية وكمات الضوء في حالات تكون فيها هذه الظواهر مهمة. أي أنه لابد من اللجوء إلى طرق ميكانيكا الكم أو الميكانيكا الموجية لتناول هذه الظواهر.

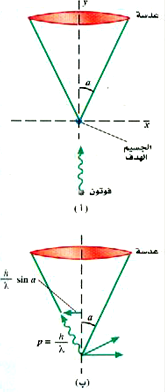
الشكل 1)): (أ) فوتون ساقط على جسيم ــ هدف. (ب) ولكي يتم اكتشاف وجود الجسيم الهدف فإن للفوتون لابد أن يخترق العدسة، التي تقابل زاوية α عند الجسيم المستهدف. ونتيجة لذلك فإن الجسيم يمكنه أن يحصل على مركبة x لكمية التحرك  تصل إلى (h/λ) sin α.