اعتماد الحرارتين النوعيتين الجزيئتين للغازات على درجة الحرارة

 أن القيم المقاسة لكل من C_V و C_P للغازات المثالية أحادية الذرة تتفق اتفاقاً جيداً مع النظرية الكلاسيكية، كما وجدنا أن النظرية الكلاسيكية لا تتنبأ بأي تغير للحرارتين النوعيتين للغازات المثالية، سواء كانت أحادية الذرة أما لا، مع درجة الحرارة. ومع ذلك فقد أثبتت التجربة أن الحرارتين النوعيتين للغازات ثنائية الذرة وعديدة الذرات تعتمد بالفعل على درجة الحرارة، وان قيمتها عند درجات الحرارة المنخفضة والمتوسطة لا تتفق مع التنبؤات الكلاسيكية. ولفهم أسباب هذا التناقض علينا أن نلجأ مرة أخرى إل مفهوم الطاقة التكممية.

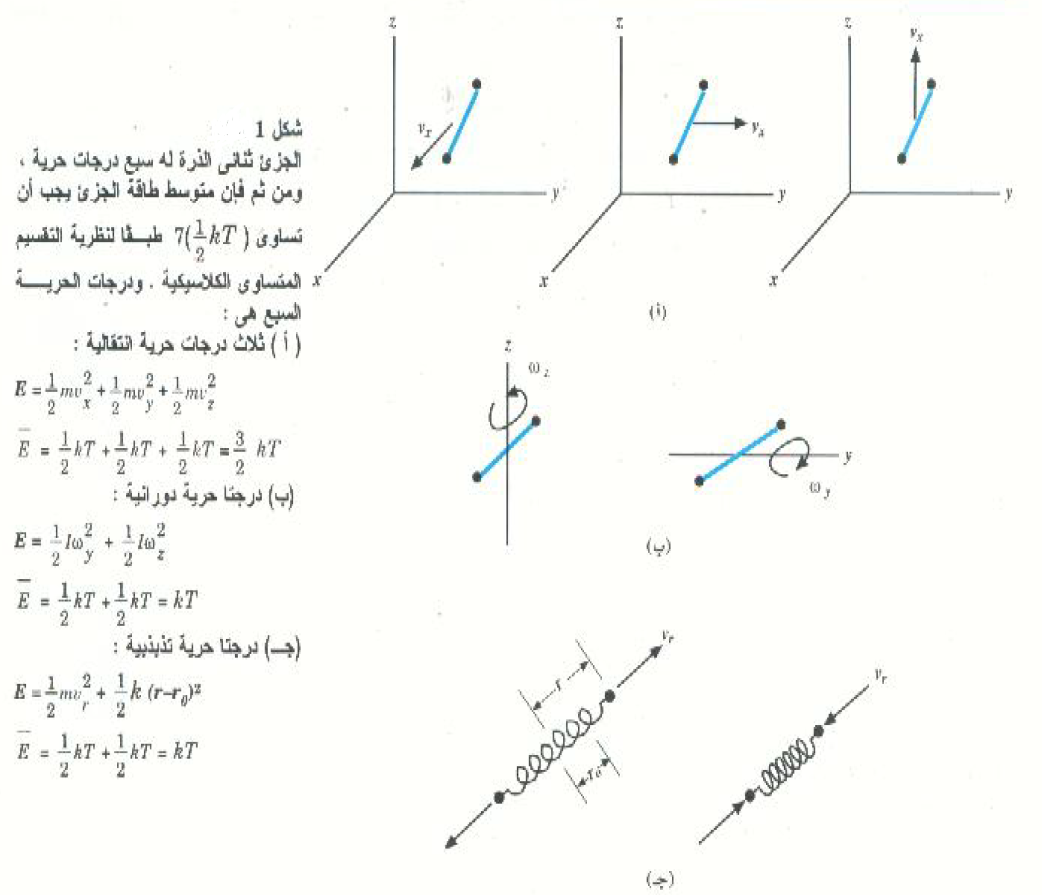
المبدأ الأساسي للاتزان الحراري هو أن كلاً من مركبات الحركة، في الاتجاهات x و y و z، تساهم بنصيب متساو في الطاقة الداخلية للغاز؛ وهذا ما يسمى نظرية التقسيم المتساوي للطاقة. وهكذا فإن كلاً من مركبات الحركة الانتقالية للذرة تساهم في طاقة الحركة الانتقالية (3kT/2) بمقدار الثلث، أي  kT½ في المتوسط؛ وسوف نسمى هذه المركبات المستقلة للحركة بدرجات حرية الغاز. ومعنى ذلك أن الغاز أحادي الذرة له 3 درجات حرية، واحدة لكل من مركبات متجه سرعته الثلاث.

ولمعالجة الغازات الجزيئية فإننا سنقوم بتعميم نظرية التقسيم المتساوي على جميع الحركات المستقلة ( درجات الحرية) التي تساهم في طاقة الجزئ. فالجزيئات الخطية ثنائية الذرة كجزئ الهيدروجين H₂ يمكنها الدوران حول محورين مستقلين متعامدين من الخط الواصل بين الذرتين، وطبقاً لنظرية التقسيم المتساوي فإن متوسط الطاقة المرتبطة بكل درجة حرية دورانية تساوي kT½. وعلاوة على ذلك فإن تذبذب الرابطة بين الذرتين يعني أن للجزئ طاقة حركة وطاقة وضع. ومرة ثانية تتنبأ نظرية التقسيم المتساوي أن متوسط كل من طاقة حركة الجزئ وطاقة وضع تساوي kT½.

وبناء على ذلك يمكننا القول أن نظرية الكلاسيكية تتنبأ بأن الطاقة الداخلية للجزيئات الخطية ثنائية الذرة تساوي 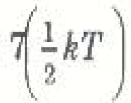لكل جزئ في المتوسط (انظر الشكل 1)))، إذن في حالة n  moles :

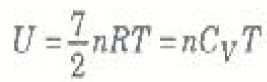
ومنه :

الآن يمكننا تفسير معنى الرمز K، حيث كتبنا التعبير العام للحرارة النوعية C_V على الصورة C_V = K(R/2) وبالنسبة  y على الصورة Y = C_p /C_v = (k+2) K من الواضح إذن أن العدد الصحيح K هو عدد درجات حرية الغاز المتاحة للمشاركة في الطاقة الحرارية. ففي حالة الغازات أحادية الذرة K = 3 ، Y = 5/3 = 1.67 ، وهذا يتفق مع التجربة. أما بالنسبة للغازات ثنائية الذرة فإن النظرية الكلاسيكية تتنبأ بأن K = 7 ، Y = 9/7 = 1.28  ، ولكن ثبت بالتجربة العلمية أن Y = 1.4 لمعظم الغازات ثنائية الذرة، وهذا يشير إل أن عدد درجات الحرية خمسة فقط (K = 5). وبالرغم من أن نتائج النظرية الكلاسيكية لا توضح أن اعتماد الحرارتين النوعيتين على درجة الحرارة، فإن القيمة العملية المقاسة لكل من C_v و C_p تؤكد أنهما تعتمدان على درجة الحرارة في حالة الغازات الجزيئية.

للنقاش الآن النتائج العملية لغاز مكون من جزيئات الهيدروجين H₂. يبين الشكل 2)) ان C_v لغاز الهيدروجين H₂ عن درجات الحرارة التي تقل عن حوالي 50K ثابتة وتساوي (3/2R) كما في حالة الغازات أحادية الذرة، وتكون(C_V = 5/2R)  فوق درجة 250 K إلى حوالي 750 K. وأخيراً تقترب C_v من قيمتها الكلاسيكية (7/2R) عند درجات الحرارة التي تزيد عن 5000 K وستنتج من هذا السلوك أن أنماط الطاقة الدورانية والتذبذبية لا تكون موجودة بالمرة عند درجات الحرارة المتوسطة. اما من وجهة النظر الكلاسيكية فإن مبدأ التوزيع المتساوي للطاقة يعني ضمنياً أن التصادمات الجزيئية تعمل على توزيع الطاقة الداخلية توزيعاً متساوياً بين جميع درجات الحرية لا يعتمد على درجة الحرارة.

ظل سلوك C_v الذي يتناقض واضحاً مع النظرية الكلاسيكية لغزاً محيراً إلى أن استطاع أينشتين تفسيره في عام 1907. ومرة أرى فإن تفسير هذا السلوك يتطلب مراجعة تفترض أنه ليس هناك أي حدود "لمدى صغر" كمية التحرك الزاوية للجسم الدائر،  وقد راينا أيضاً ان هذا الفرض يجل نبذه تماماً في حالة الأجسام ذات الأبعاد الذرية. ذلك أن خبرتنا مع الأجسام الماكروسكوبية الدائرة لا تدل إطلاقاً على أن هذا  الفرض قد يكون موضع شك. فعجلة السيارة مثلاً يمكنها أن تدور بمعدل أبطأ فأبطأ وبصورة ملساء مستمرة أثناء تقاصر السيارة إلى أن تتوقف تماماً. وبالمثل، فليس هناك في خبرتنا مع الأنظمة المتذبذبة، كالزنبرك والبندول، ما يحملنا على الاعتقاد بأن هناك حداً يختلف عن الصفر فيما يتعلق بالتردد الادنى الممكن للتذبذب. ومن الغريب حقاً ان أكثر الفروض "وضوحاً" تكون هي الأصعب اختباراً في معظم الاحيان.

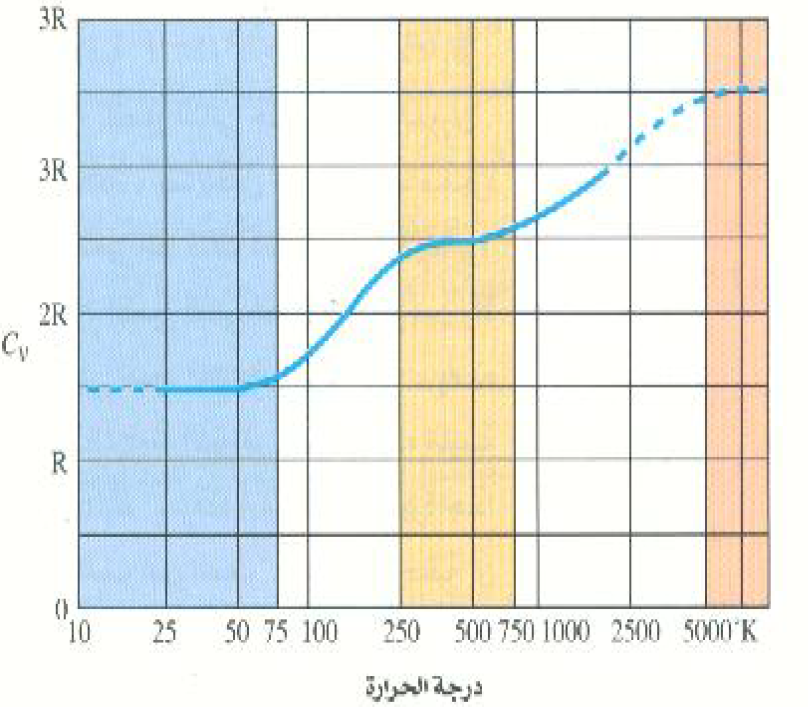
الشكل 2)): القيم العملية للحرارة النوعية Cv لغاز الهيدروجين ثنائي الذرة كدالة في درجة الحرارة. لاحظ التدريج اللوغاريتمي لمحوري الإحداثيات.

أن كمية التحرك الزاوي للأجسام الدائرة فائقة الصغر ظاهرة تكممية، وأن كم كمية التحرك الزاوي يساوي .(L₁ = h/2 π) هذا يعني أن الطاقة الدورانية الدنيا لمثل هذه الأجسام تعطي بالعلاقة 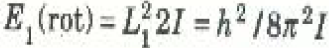.حيث h ثابت بلانك (6.62×10^-34 J.s) و I عزم القصور الذاتي حول محور الدوران.

أن ثابت بلانك h يظهر مربعاً في هذه العلاقة، مما يجعل قيمة البسط صغيرة جداً. ومع ذلك فإن عزم القصور الذاتي للجزيئات صغيرة جداً كذلك لأنه يتضمن كتلاً صغيرة  جداً ومسافات صغيرة جداً بين الذرات. فمثلاً، عزم القصور الذاتي لجزئ الهيدروجين H₂ حول محور عمودي على الرابطة بين الذرتين  H في حدود I = 10^-47 kg m²، وهذه قيمة متناهية الصغر بالمقاييس الماكروسكوبية. ولذلك فعند التعويض عن I بهذه القيمة في معادلةE₁(rot)  سنحصل على E₁(rot)=10^-21J ، وهذه أيضاً كمية صغيرة جداً بالمقياس الماكروسكوبي بحيث لا نحس أنها تختلف عن الصفر. ولكن بملاحظة أن ثابت بولتزمان ، الذي يحدد كمية الطاقة الحرارية المتاحة لكل درجة حرية، أصغر كثيراً من ذلك (في حدود J/k 10^-23)، ويساويKT تقريباً عندما T = 100 K.

وفي عام 1907 افترض أينشتاين أن الطاقات الممكنة لجزئ متذبذب يمكن أن تكون تكممية أيضاً، بمعنى ان الطاقات التذبذبية لا يمكن أن تكون صغيرة بلا حدود، بل إنها تساوي مضاعفات لكمية أساسية من الطاقة لا يمكن تقسيمها. كذلك افترض أينشتين أن كم الطاقة التذبذبية يتناسب مع تردد التذبذب f وأن ثابت التناسب يساوي ثابت بلانك. ويمكن التعبير عن ذلك رياضياً بالمعادلة E_asc = n(hf) حيث n عدد صحيح (h = 6.62×10^-34 J.s) ( أو J/Hz) مرة ثانية. وطبقاً لهذه الفكرة فإن طاقة المتذبذب لا يمكن ان تكون أصغر من E₁ (vib) = hf. وفي حالة المتذبذبات الماكروسكوبية الكبيرة تكون الترددات مع الصغر بحيث تصبح hf كما صغيراً جداً. أي أنه يمثل كمية متناهية الصغر من الطاقة يستحيل قياسها. اما في حالة الاهتزازات الجزيئية ذات الترددات العالية جداً فإن الكمية hf تمثل "كتلة كبيرة" من الطاقة على هذا المقياس.

لنحاول الآن أن نرى كيف يمكن تفسير سلوك الحرارتين النوعيتين باستخدام مفهوم كمات الطاقة الدورانية والاهتزازية. ويجب أن نتذكر بداية أن التصادمات بين الجزيئات هي التي تسبب توزيع الطاقة الحرارية توزيعاً إحصائياً بين أنماط الطاقة الجزيئية المختلفة، وأن متوسط الطاقة المتبادلة بين الجزيئات المتصادمة يساوي kT تقريباً. هذه الطاقة تكون صغيرة جداً عند درجات الحرارة فائقة الانخفاض. فإذا كانت درجة حرارة الغاز منخفضة جداً فإن الطاقة المتبادلة في تصادم متوسط (=kT) تكون أصغر من كم الطاقة الدورانية (h²/8π² I)، وبذلك لن تكون كافية لأن يبدأ الجزئ في الدوران على الإطلاق. وعليه، فإذا كانت درجة الحرارة أقل من

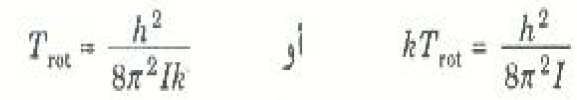
تقريباً، ستكون درجتا الحرة الدورانيتان "متجمدتين" ولن تساهما في الحرارة النوعية للغاز؛ ويوضح الجدول 1)) بعض قيم T_rot لاحظ أن T_rot لجزئ H₂.

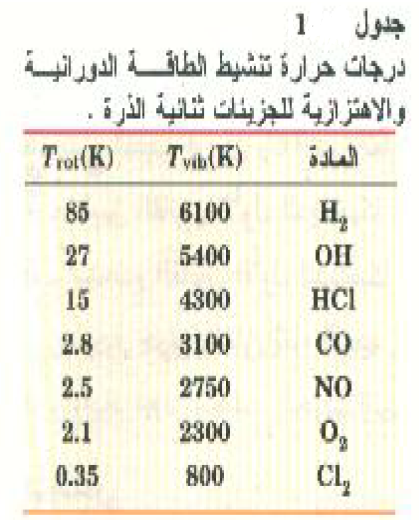
وبالمثل، عندما تكون درجة حرارة الغاز منخفضة بدرجة كافية لأن تكون الطاقة المنتقلة KT في تصادم متوسط أقل من الكم hf اللازم لاهتزاز الرابطة بين الذرتين، فإن التصادمات المتوسطة لن يمكنها "تنشيط" الاهتزازات الجزيئية، وبذلك لن يشارك النمطان الاهتزازيان للطاقة في الحرارة النوعية. هذا يعني إحصائياً أنه ما لم تصل درجة حرارة الغاز إلى