
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الطاقة الحرة
المؤلف:
بيتر أتكينز
المصدر:
الكيمياء الفيزيائية
الجزء والصفحة:
ص 36 – ص 40
2024-10-01
1356
ثمة شرَك هنا. ففي جميع المراجع الخاصة بالديناميكا الحرارية الكيميائية، يجري التأكيد على انه من أجل استخدام القانون الثاني من الضروري الوضع في الاعتبار إجمالي التغير في الإنتروبي، أي مجموع التغيرات داخل النظام (مزيج التفاعل) ووسطه المحيط. يمكن استنتاج الأولى من جداول قيم الإنتروبي التي جرى تجميعها، ولكن كيف تُحسب الثانية؟
هذا هو الموضع الذي يعود فيه الإنثالبي ليلعب دورًا فإذا كنا نعرف التغير في الإنثالبي الحادث أثناء تفاعل ما فعندئذٍ سنعرف مقدار الطاقة المنبعثة على هيئة حرارة إلى الوسط المحيط، هذا بشرط أن تتم العملية تحت ضغط ثابت. وإذا قسمنا انتقال حرارة هذا على درجة الحرارة، فسنحصل على التغير في الإنتروبي في الوسط المحيط. وبالتالي، إذا تراجع الإنثالبي الخاص بنظام ما بمقدار 100 جول أثناء تفاعل يحدث عند درجة حرارة 25 درجة مئوية (298) كلفن، فإن المائة جول هذه تترك النظام على هيئة حرارة وتدخل إلى الوسط المحيط وبالتالي يزيد الإنتروبي الخاص بها بمقدار 0.34 جول لكل كلفن. كل ما علينا أن نفعله هو أن نجمع تغيُّري الإنتروبي، ذلك الخاص بالنظام والآخر الخاص بالوسط المحيط، معًا، ونحدد ما إذا كان إجمالي التغير موجبًا (التفاعل تلقائي) أم سالبًا (التفاعل غير تلقائي).
لقد وجد علماء الكيمياء الفيزيائية طريقة ذكية لتحديد الجزئية المزعجة من عملية الحساب هذه والمتمثلة في تقييم التغير في الإنتروبي الخاصة بالوسط المحيط. في واقع الأمر، وإحقاقا للحق، يعود الفضل إلى عالم فيزياء نظرية آخر ألا وهو الأمريكي جوسايا جيبس (1839–1903) الذي سلط الضوء على الديناميكا الحرارية في سبعينيات القرن التاسع عشر حيث أمكن اعتبارها أحد جوانب الكيمياء الفيزيائية، وأسس بفعالية لهذا الفرع من المجال. مرة أخرى، نرى أن الفيزياء توفر نقطة انطلاق لإحراز التقدم في الكيمياء الفيزيائية.
لاحظ جيبس أن التغيرين في الإنتروبي، الخاص بالنظام والخاص بالوسط المحيط، يمكن حسابهما من خلال التركيز فقط على تغيرات ما نطلق عليه الآن «طاقة جيبس»، ويرمز لها بـ G، الخاصة بالنظام وظاهريا تجاهل الوسط المحيط تماما، بشرط أن يكون الضغط ودرجة الحرارة ثابتين. تذكر كيف يُحسب الإنثالبي من خلال جمع حاصل ضرب ضغط النظام في حجمه pV والطاقة الداخلية (H = U + pV) U؛ وعلى نحو مماثل تحسب طاقة جيبس لنظام ما من خلال طرح حاصل ضرب درجة الحرارة والإنتروبي من الإنثالبي: G = H – TS. على سبيل المثال، إنتروبي 100 مليلتر من الماء عند درجة حرارة 20 درجة مئوية (293) كلفن هو 0.388 كيلو جول لكل كلفن، وبالتالي طاقة جيبس الخاصة بها هي أقل بنحو 114 كيلو جول من الإنثالبي الخاص بها، أيا ما كان.
غير أن الأرقام الفعلية لا تخدم أغراضنا هنا بصفة خاصة؛ وإنما الذي يهمنا أكثر هو وجود علامة الناقص في المعادلة: G = H – TS. عندما تُحلل هذه المعادلة، يتضح أن التغير التلقائي يكافئه انخفاض في طاقة جيبس، بشرط أن يكون الضغط ودرجة الحرارة ثابتين. وهذا يجعل طاقة جيبس الخاصة بالنظام وحدها مؤشرا على التغير التلقائي: كل ما نحتاج إليه هو تجميع جداول قيم طاقة جيبس لقيم الإنثالبي والإنتروبي، ومعرفة الطريقة التي تتغير بها طاقة جيبس في التفاعل وملاحظة ما إذا كان التغير سالبًا. فإذا كان سالبًا، فيكون التفاعل تلقائيا (انظر شكل 2–3).
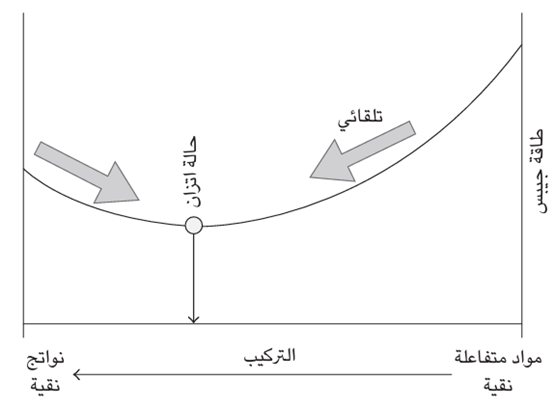
شكل 2–3: يكون التفاعل تلقائيا عندما تتجه طاقة جيبس نحو الانخفاض. وعندما تكون طاقة جيبس في أدنى مستوياتها، يكون التفاعل في حالة اتزان مع غياب النزعة للتغير نحو أي من الاتجاهين.
ويتعين علي هنا أن أدلي بملاحظة أخرى. فعلى الرغم من أنه يبدو أن من البديهي أكثر اعتبار عملية ما طبيعيةً إذا كانت تتضمن «انخفاضًا» في خاصية ما، في هذه الحالة طاقة جيبس، فيجب أن نتذكر أن طاقة جيبس هي نسخة متخفية من الإنتروبي الإجمالي. ويكون الاتجاه التلقائي للتغير إلى «أعلى» على نحو ثابت بالنسبة إلى الإنتروبي الإجمالي. أوضح جيبس للكيميائيين أنهم في مقابل التخلي عن التعميم والتعامل فقط . مع التغيرات عند درجة حرارة وضغط ثابتين، يستطيعون التعامل مع خاصية واحدة للنظام، ألا وهي طاقة جيبس، وببساطة وبحكم تعريفها، مع وجود علامة الناقص، يعني «الانخفاض» في طاقة جيبس «الارتفاع» في الإنتروبي الإجمالي.
ثمة جانب مهم جدًّا خاص بالتلقائية يجب علي أن أطرحه الآن. يولي الكيميائيون اهتمامًا بالغًا بالتركيب الذي يختفي عندها ميل أي تفاعل كيميائي نحو التغير: وهذا ما يُعرف بـ «حالة الاتزان الكيميائي». ولا يكون التفاعل الأمامي أو العكسي تلقائيا عندما يصل المزيج إلى حالة الاتزان بعبارة أخرى، عند التركيب المكافئ لحالة الاتزان، لا يوازي أي تغير في البنية، سواء أتمثل هذا التغير في تكوين المزيد من النواتج أم تحللها، انخفاضًا في طاقة جيبس : لقد وصلت طاقة جيبس إلى أدنى مستوى مع الوضع في الاعتبار أن التغير في أي من الاتجاهين يوازي زيادة في طاقة جيبس. وكل ما يجب على علماء الكيمياء الفيزيائية القيام به من أجل توقع التركيب في حالة الاتزان هو تحديد التركيب الذي تصل عنده طاقة جيبس إلى أدنى مستوى. وثمة طرق مباشرة لإجراء تلك العملية الحسابية، ويمكن حساب تركيب حالة الاتزان لأي تفاعل تقريبًا عند أية درجة حرارة بشرط أن تتوفر البيانات الخاصة بطاقة جيبس.
والقدرة على توقع تركيب حالة الاتزان الخاصة بأي تفاعل وإلى أي مدى يعتمد على الظروف لهي أمر ذو أهمية بالغة في مجال الصناعة، نظرًا إلى أنه لا جدوى من بناء مصنع كيميائي إذا كان عائد النواتج لا يُذكر، وتعول الاعتبارات الاقتصادية على توفير ظروف درجة الحرارة والضغط التي قد تؤدي إلى تحسين العوائد.
أخيرًا، يتعين علي شرح مصطلح «الطاقة الحرة» الذي اتخذت منه عنوانًا لهذا القسم وبهذا أفتح بابًا آخر مهما أمام التطبيقات البيولوجية والتكنولوجية للقانون الثاني للديناميكا الحرارية.
ثمة نوعان من الشغل. النوع الأول هو الشغل المبذول أثناء التمدد الذي يحدث عندما يولد التفاعل غازًا ويقاوم الضغط الجوي (ربما) من خلال الضغط على مكبس). يُسمى هذا النوع «الشغل التمددي». ولكن ربما يبذل التفاعل شغلًا آخر غير ذلك المبذول من خلال الضغط على مكبس أو مقاومة الضغط الجوي. فعلى سبيل المثال، ربما يبذل شغلًا من خلال دفع الإلكترونات عبر دائرة كهربائية متصلة بمحرك . وهذا النوع من الشغل يُطلق عليه «الشغل اللاتمددي». والآن نأتي إلى النقطة المهمة هنا: التغير في طاقة جيبس الخاصة بنظام ما عند درجة حرارة وضغط ثابتين يعادل الحد الأقصى للشغل اللاتمددي الذي يمكن بذله من جانب التفاعل. ومن ثم، تفاعل تقل فيه طاقة جيبس بمقدار 100 جول يمكن أن يبذل شغلًا لا تمدديًا حتى 100 جول. وهذا الشغل اللاتمددي ربما يكون الشغل الكهربائي الخاص بدفع الإلكترونات عبر دائرة خارجية. وهكذا، نصل إلى حلقة وصل مهمة بين الديناميكا الحرارية و«الكيمياء الكهربائية»، التي تشمل توليد الكهرباء من خلال التفاعلات الكيميائية وعلى وجه التحديد آلية عمل البطاريات الكهربائية وخلايا الوقود.
وثمة حلقة وصل أخرى مهمة تكشفها هذه العلاقة فالصلة التي تربط الديناميكا الحرارية وعلم الأحياء هي أن التفاعل الكيميائي ربما يبذل الشغل اللاتمددي الخاص ببناء أحد البروتينات من الأحماض الأمينية. لذا، فإن معرفة التغيرات في طاقة جيبس المصاحبة لعمليات الأيض مهمة جدًّا في علم الطاقة الحيوية، وأهم بكثير من معرفة التغيرات في الإنثالبي وحدها (التي تشير فقط إلى قدرة التفاعل على شعورنا بالدفء). وتعد هذه الصلة إسهامًا كبيرًا تقدمه الكيمياء الفيزيائية إلى مجال الكيمياء الحيوية وعلم الأحياء بوجه عام.
 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)

















