The Fibonacci sequence of whole numbers is:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, . . .

The sequence is widely known for its many intriguing properties. The most basic – indeed the characteristic feature which defines them – is that every term is the addition of the previous two. For example 8 = 5 + 3, 13 = 8 + 5, . . ., 2584 = 1587 + 987, and so on. All you have to remember is to begin with the two numbers 1 and 1 and you can generate the rest of the sequence on the spot. The Fibonacci sequence is found in nature as the number of spirals formed from the number of seeds in the spirals in sunflowers (for example, 34 in one direction, 55 in the other), and the room proportions and building proportions designed by architects. Classical musical composers have used it as an inspiration, with Bartók’s Dance Suite believed to be connected to the sequence. In contemporary music Brian Transeau (aka BT) has a track in his album This Binary Universe called 1.618 as a salute to the ultimate ratio of the Fibonacci numbers, a number we shall discuss a little later.

Origins

The Fibonacci sequence occurred in the Liber Abaci published by Leonardo of Pisa (Fibonacci) in 1202, but these numbers were probably known in India before that. Fibonacci posed the following problem of rabbit generation:

Mature rabbit pairs generate young rabbit pairs each month. At the beginning of the year there is one young rabbit pair. By the end of the first month they will have matured, by the end of the second month the mature pair is still there and they will have generated a young rabbit pair. The process of maturing and generation continues. Miraculously none of the rabbit pairs die.

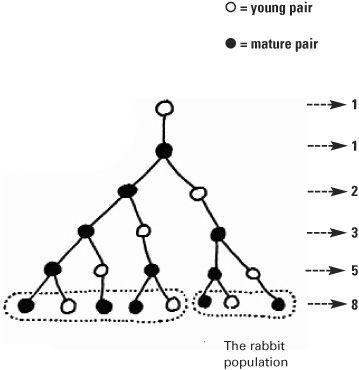
Fibonacci wanted to know how many rabbit pairs there would be at the end of the year. The generations can be shown in a ‘family tree’. Let’s look at the number of pairs at the end of May (the fifth month). We see the number of pairs is 8. In this layer of the family tree the left-hand group

is a duplicate of the whole row above, and the right-hand group

is a duplicate of the row above that. This shows that the birth of rabbit pairs follows the basic Fibonacci equation:

number after n months = number after (n – 1) month
+ number after (n – 2) months

Properties

Let’s see what happens if we add the terms of the sequence:

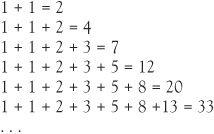
The result of each of these sums will form a sequence as well, which we can place under the original sequence, but shifted along:

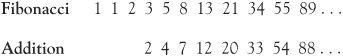
The addition of n terms of the Fibonacci sequence turns out to be 1 less than the next but one Fibonacci number. If you want to know the answer to the addition of 1 + 1 + 2 + . . . + 987, you just subtract 1 from 2584 to get 2583. If the numbers are added alternately by missing out terms, such as 1 + 2 + 5 + 13 + 34, we get the answer 55, itself a Fibonacci number. If the other alternation is taken, such as 1 + 3 + 8 + 21 + 55, the answer is 88 which is a Fibonacci number less 1.

The squares of the Fibonacci sequence numbers are also interesting. We get a new sequence by multiplying each Fibonacci number by itself and adding them.

In this case, adding up all the squares up to the nth member is the same as multiplying the nth member of the original Fibonacci sequence by the next one to this. For example,

1 + 1 + 4 + 9 + 25 + 64 + 169 = 273 = 13 × 21

Fibonacci numbers also occur when you don’t expect them. Let’s imagine we have a purse containing a mix of £1 and £2 coins. What if we want to count the number of ways the coins can be taken from the purse to make up a particular amount expressed in pounds. In this problem the order of actions is important. The value of £4, as we draw the coins out of the purse, can be any of the following ways, 1 + 1 + 1 + 1; 2 + 1 +1; 1 + 2 + 1; 1 + 1 + 2; and 2 + 2. There are 5 ways in all – and this corresponds to the fifth Fibonacci number. If you take out £20 there are 6,765 ways of taking the £1 and £2 coins out, corresponding to the 21st Fibonacci number! This shows the power of simple mathematical ideas.

The golden ratio

If we look at the ratio of terms formed from the Fibonacci sequence by dividing a term by its preceding term we find out another remarkable property of the Fibonacci numbers. Let’s do it for a few terms 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

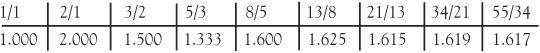
Pretty soon the ratios approach a value known as the golden ratio, a famous number in mathematics, designated by the Greek letter Φ. It takes its place amongst the top mathematical constants like π and e, and has the exact value

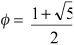
and this can be approximated to the decimal 1.618033988. . . With a little more work we can show that each Fibonacci number can be written in terms of Φ.

The cattle population

Despite the wealth of knowledge known about the Fibonacci sequence, there are still many questions left to answer. The first few prime numbers in the Fibonacci sequence are 2, 3, 5, 13, 89, 233, 1597 – but we don’t know if there are infinitely many primes in the Fibonacci sequence.

Family resemblances

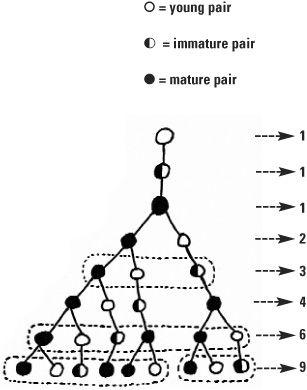
The Fibonacci sequence holds pride of place in a wide ranging family of similar sequences. A spectacular member of the family is one we may associate with a cattle population problem. Instead of Fibonacci’s rabbit pairs which transform in one month from young pair to mature pair which then start breeding, there is an intermediate stage in the maturation process as cattle pairs progress from young pairs to immature pairs and then to mature pairs. It is only the mature pairs which can reproduce. The cattle sequence is:

1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595, . . .

Thus the generation skips a value so for example, 41 = 28 + 13 and 60 = 41 + 19. This sequence has similar properties to the Fibonacci sequence. For the cattle sequence the ratios obtained by dividing a term by its preceding term approach the limit denoted by the Greek letter psi, written ψ, where

ψ = 1.46557123187676802665. . .

This is known as the ‘supergolden ratio’.

the condensed idea

The Da Vinci Code unscrambled

مواضيع ذات صلة

π

Zero

Triangles

Topology

The travelling salesperson

The Riemann hypothesis

The parallel postulate

The normal curve

The four-colour problem

The diet problem

The birthday problem

Squares and square roots