

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Money mathematics
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
252-256
25-2-2016
2070
Norman is a super salesperson when it comes to bikes. He also sees it as his duty to get everyone on a bike, so he is delighted when a customer comes into his shop and without any hesitation buys a bike for £99. The customer pays for it with a cheque for £150, and as the banks are closed, Norman asks his neighbour to cash it. He returns, gives his customer the change of £51 who then rides off at speed. Calamity follows. The cheque bounces, the neighbour demands his money back, and Norman has to go to a friend to borrow the money. The bike originally cost him £79, but how much did Norman lose altogether?
The concept of this little conundrum was proposed by the great puzzlesmith Henry Dudeney. It is money mathematics of a sort, but more accurately a puzzle connected with money. It shows how money depends on time and that inflation is alive and well. Writing in the 1920s, Dudeney’s bike actually cost the customer £15. A way to combat inflation is through the interest on money. This is the stuff of serious mathematics and the modern financial market place.
Compound interest
There are two sorts of interest, known as simple and compound. Let’s turn our mathematical spotlight onto two brothers, Compound Charlie and Simple Simon. Their father gives them each £1000, which they both place in a bank. Compound Charlie always chooses an account that applies compound interest but Simple Simon is more traditional and prefers accounts that use simple interest. Historically, compound interest was identified with usury and frowned upon. Nowadays compound interest is a fact of life, central to modern monetary systems. Compound interest is interest compounded on interest, and that is why Charlie likes it. Simple interest does not have this feature and is calculated on a set amount known as the ‘principal’. Simon can understand it easily, as the principal earns the same amount of interest each year.
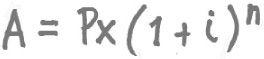
Compound interest formula
When talking about mathematics, it is always good to have Albert Einstein on side – but the widespread claim that he said compound interest is the greatest discovery of all time is too far-fetched. That the formula for compound interest has a greater immediacy than his E = mc2 is undeniable. If you save money, borrow money, use a credit card, take out a mortgage or buy an annuity, the compound interest formula is in the background working for (or against) you. What do the symbols stand for? The term P stands for principal (the money you save or borrow), i is the percentage interest rate divided by 100 and n is the number of time periods.
Charlie places his £1000 in an account paying 7% interest annually. How much will accrue in three years? Here P = 1000, i = 0.07 and n = 3. The symbol A represents the accrued amount and by the compound interest formula A=£1225.04.
Simon’s account pays the same interest rate, 7%, as simple interest. How do his earnings compare after three years? For the first year he would gain £70 in interest and this would be the same in the second and third years. He would therefore have 3 × £70 interest giving a total accrued amount of £1210. Charlie’s investment was the better business decision.
Sums of money that grow by compounding can increase very rapidly. This is fine if you are saving but not so good if you are borrowing. A key component of compound interest is the period at which the compounding takes place. Charlie has heard of a scheme which pays 1% per week, a penny in every pound. How much would he stand to gain with this scheme?
Simon thinks he knows the answer: he suggests we multiply the interest rate 1% by 52 (the number of weeks in the year) to obtain an annual percentage rate of 52%. This means an interest of £520 making a total of £1520 in the account. Charlie reminds him, however, of the magic of compound interest and the compound interest formula. With P = £1000, i = 0.01 and n = 52, Charlie calculates the accrual to be £1000 × (1.01)52. Using his calculator he finds this is £1677.69, much more than the result of Simple Simon’s sum. Charlie’s equivalent annual percentage rate is 67.769% and is much greater than Simon’s calculation of 52%.
Simon is impressed but his money is already in the bank under the simple interest regime. He wonders how long it will take him to double his original £1,000? Each year he gets £70 interest so all he has to do is divide 1000 by 70. This gives 14.29 so that he can be sure in 15 years he will have more than £2000 in the bank. It is a long time to wait. To show the superiority of compound interest Charlie starts to calculate his own doubling period. This is a little more complicated but a friend tells him about the rule of 72.
The rule of 72
For a given percentage rate, the rule of 72 is a rule of thumb for estimating the number of periods required for money to double. Though Charlie is interested in years the rule of 72 applies to days or month as well. To find the doubling period all Charlie has to do is to divide 72 by the interest rate. The calculation is 72/7 = 10.3 so Charlie can report to his brother that his investment will double in 11 years, much quicker than Simon’s 15. The rule is an approximation but it is useful where quick decisions have to be made.
Present value Compound Charlie’s father is so impressed by his son’s good sense that he takes him aside and says ‘I propose to give you £100,000’. Charlie is very excited. Then his father adds the condition that he will only give him the £100,000 when he is 45 and that won’t be for another ten years. Charlie is not so happy.
Charlie wants to spend the money now but obviously he cannot. He goes to his bank and promises them the £100,000 in ten years time. The bank responds that time is money and £100,000 in ten years time is not the same as £100,000 now. The bank has to estimate the size of investment now that would realize £100,000 in ten years. This will be the amount they will loan to Charlie. The bank believes that a growth rate of 12% would give them a healthy profit. What would be the amount now that would grow to £100,000 in ten years, at 12% interest? The compound interest formula can be used for this problem as well. This time we are given A = £100,000 and have to calculate P, the present value of A. With n = 10 and i = 0.12, the bank will be prepared to advance Charlie the amount 100,000/1.1210 = £32,197.32. Charlie is quite shocked by this small figure, but he will still be able to buy that new Porsche.
How can regular payments be handled?
Now that Charlie’s father has promised to give £100,000 to his son in ten years time, he has to save the money up. This he plans to do with a stream of equal saving account payments made at the end of each year for ten years. By the end of this period he will then be able to hand over the money to Charlie on the day he has promised, and Charlie can hand the money to the bank to pay off the loan.

Regular payments formula
Charlie’s father manages to find an account that allows him to do this, an account that pays an annual interest rate of 8% for the whole ten year term. He gives Charlie the task of working out the annual payments. With the compound interest formula Charlie was concerned with one payment (the original principal) but now he is concerned with ten payments made at different times. If regular payments R are made at the end of each year in an environment where the interest rate is i, the amount saved after n years can be calculated by the regular payments formula.
Charlie knows that S = £100,000, n = 10 and i = 0.08 and calculates that R = £6902.95.
Now that Charlie has his brand new Porsche, courtesy of the bank, he needs a garage to put it in. He decides to take out a mortgage for £300,000 to buy a house, a sum of money he will pay back in a stream of equal annual payments over 25 years. He recognizes this as a problem in which the £300,000 is the present value of a stream of payments to be made and he calculates his annual payments with ease. His father is impressed and makes further use of Charlie’s prowess. He has just been given a retirement lump sum of £150,000 and wants to purchase an annuity. ‘That’s OK,’ says Charlie, ‘we can use the same formula, as the mathematics is the same. Instead of the mortgage company advancing me money that I repay in regular instalments, you are giving them the money and they are making the regular payments to you.’
By the way, the answer to Henry Dudeney’s brainteaser is £130, made up of the £51 Norman gave the customer and the £79 he paid for the bike.
the condensed idea
Compound interest works best

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















