
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
المتجهات الأحادية (The Unit Vectors)
المؤلف:
د. معن صفاء ابراهيم
المصدر:
الفيزياء الجامعية 101
الجزء والصفحة:
ص 29
23-2-2016
9291
المتجهات الأحادية (The Unit Vectors)
وهو متجه له قيمة تساوي وحدة واحدة من وحدات القياس ويستخدم ليشير إلى اتجاه الحركة على المحور السيني أو الصادي أو على المحور العمود (z-axis). وعلى هذا الأساس يرمز للمتجه الأحادي باتجاه المحور السيني بــ (i)، وباتجاه المحور الصادي بــ (j) وباتجاه العمود بــ (K) كما في الشكل (1.1). ويمكن الاستفادة من المتجه الاحادي لإعطاء تعريف آخر لمركبات المتجه حيث تعرف المركبة بذكر القيمة وذكر المتجه الموحد. فعلى سبيل المثال يمكن كتابة المتجهA في المستوى x-y بدلالة مركباته وبدلالة المتجه الموجد على النحو التالي:
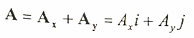
حيث Ax ، Ay تمثل قيمة مركبات المتجه على المحور السيني والصادي، وان i، j تمثل اتجاه المركبتين على المحور السيني والصادي بالتعاقب. وإذا كان الجسم يتحرك على ثلاثة محاور فيمكن كتابة معادلة المتجه A باتجاه المحاور الثلاثة كما يلي:
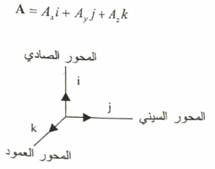
الشكل (1.1) يمثل المتجهات الأحادية
الشكل رقم (1.2) يمثل المتجهان A،B في المستوى x-y ولإيجاد محصلة المتجهان (R) باستخدام مفهوم المتجه الموجد يمكن كتابة معادلتهما بدلالة المتجه الموحد كما يلي:
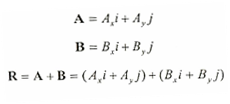
ويمكن فصل تبسيط المعادلة كما يلي:
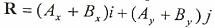
ويمكن وضعها بالصيغة التالية:
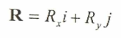
حيث Ry = Ay + By , Rx = Ax + Bx وهي مركبات متجه المحصلة (R) باتجاه المحور السيني والصادي على التعاقب، ويمكن حساب قيمة تلك المحصلة حسب نظرية فيثاغورس كما يلي:
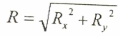
كذلك يمكن إيجاد ظل زاوية ميل المحصلة عن المحور السيني كما يلي:
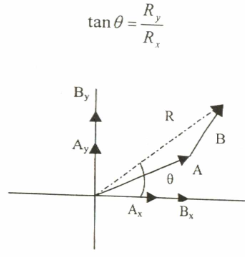
الشكل (1.2) يمثل تحليل المتجهات إلى مركباتها.
فإذا كان الجسم يتحرك بمتجه على ثلاثة أبعاد فإن المحصلة يمكن حسابها كما يلي:
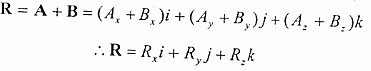
وتكون قيمة المحصلة كما يلي:
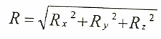
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















