

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Genetics
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
2014-2018
23-2-2016
1674
Genetics is a branch of biology, so why is it in a mathematics book? The answer is that these two subjects cross-fertilize and enrich each other. The problems of genetics require mathematics but genetics has also suggested new branches of algebra. Gregor Mendel is central to the whole theme of genetics, the study of human inheritance. Hereditary characteristics such as eye colour, hair colour, colourblindness, left/right-handedness and blood group types are all determined by factors (alleles) of a gene. Mendel said that these factors pass independently into the next generation.
So how could eye-colour factor be transmitted to the next generation? In the basic model there are two factors, b and B:
b is the blue eyes factor
B is the brown eyes factor
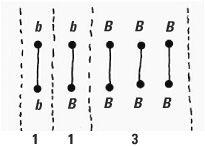
Population representing the proportions 1:1:3 of genotypes bb, bB and BB
In individuals, the factors appear in pairs giving rise to possible genotypes bb, bB and BB (because bB is the same as Bb). A person carries one of these three genotypes, which determines their eye colour. For example, a population could consist of a fifth of people with the genotype bb, another fifth with the genotype bB and the remaining three-fifths with the genotype BB. In terms of percentages, these genotypes would make up 20%, 20% and 60% of the population. This can be represented by a diagram showing these proportions of genotypes.
The factor B, which denotes brown eye colour, is the dominant factor and b, the blue eye colour is the recessive factor. A person with a pure genes genotype BB will have brown eyes, but so too will a person with mixed factors, that is, those with a hybrid genotype bB because B is dominant. A person with the pure genes genotype bb will be the only genotype to show blue eyes.
A burning question in the field of biology arose at the beginning of the 19th century. Would brown eyes eventually take over and blue eyes die out? Would blue eyes become extinct? The answer was a resounding ‘No’.
The Hardy–Weinberg law
This was explained by the Hardy–Weinberg law, an application of basic mathematics to genetics. It explains how, in the Mendelian theory of inheritance, a dominant gene does not take over completely and a recessive gene does not die out.
G.H. Hardy was an English mathematician who prided himself on the non-applicability of mathematics. He was a great researcher in pure mathematics but is probably more widely known for this single contribution to genetics – which started life as a piece of mathematics on the back of an envelope done after a cricket match. Wilhelm Weinberg came from a very different background. A general medical practitioner in Germany, he was a geneticist all his life. He discovered the law at the same time as Hardy, around 1908.
The law relates to a large population in which mating happens at random. There are no preferred pairings so that, for instance, blue-eyed people do not prefer to mate with blue-eyed people. After mating, the child receives one factor from each parent. For example, a hybrid genotype bB mating with a hybrid bB can produce any one of bb, bB, BB, but a bb mating with a BB can only produce a hybrid bB. What is the probability of a b-factor being transmitted? Counting the number of b-factors there are two b-factors for each bb genotype and one b factor for each bB genotype giving, as a proportion, a total of three b-factors out of 10 (in our example of a population with 1:1:3 proportions of the three genotypes). The transmission probability of a b-factor being included in the genotype of a child is therefore 3/10 or 0.3. The transmission probability of a B-factor being included is 7/10 or 0.7. The probability of the genotype bb being included in the next generation, for example, is therefore 0.3 × 0.3 = 0.09. The complete set of probabilities is summarized in the table.

The hybrid genotypes bB and Bb are identical so the probability of this occurring is 0.21 + 0.21 = 0.42. Expressed as percentages, the ratios of genotypes bb, bB and BB in the new generation are 9%, 42% and 49%. Because B is the dominant factor, 42% + 49% = 91% of the first generation will have brown eyes. Only an individual with genotype bb will display the observable characteristics of the b factor, so only 9% of the population will have blue eyes.
The initial distribution of genotypes was 20%, 20% and 60% and in the new generation the distribution of genotypes is 9%, 42% and 49%. What happens next? Let’s see what happens if a new generation is obtained from this one by random mating. The proportion of b-factors is 0.09 + ½ × 0.42 = 0.3, the proportion of B-factors is ½ × 0.42 + 0.49 = 0.7. These are identical to the previous transmission probabilities of the factors b and B. The distribution of genotypes bb, bB and BB in the further generation is therefore the same as for the previous generation, and in particular the genotype bb which gives blue eyes does not die out but remains stable at 9% of the population. Successive proportions of genotypes during a sequence of random matings are therefore
20%, 20%, 60% → 9%, 42%, 49% → . . . → 9%, 42%, 49%
This is in accordance with the Hardy–Weinberg law: after one generation the genotype proportions remain constant from generation to generation, and the transmission probabilities are constant too.
Hardy’s argument
To see that the Hardy–Weinberg law works for any initial population, not just the 20%, 20% and 60% one that we selected in our example, we can do no better than refer to Hardy’s own argument which he wrote to the editor of the American journal Science in 1908.
Hardy begins with the initial distribution of genotypes bb, bB and BB as p, 2r and q and the transmission probabilities p + r and r + q. In our numerical example (of 20%, 20%, 60%), p = 0.2, 2r = 0.2 and q = 0.6. The transmission probabilities of the factors b and B are p + r = 0.2 + 0.1 = 0.3 and r + q = 0.1 + 0.6 = 0.7. What if there were a different initial distribution of the genotypes bb, bB and BB and we started with, say, 10%, 60% and 30%? How would the Hardy–Weinberg law work in this case? Here we would have p = 0.1, 2r = 0.6 and q = 0.3 and the transmission probabilities of the factors b and B are respectively p + r = 0.4 and r + q = 0.6. So the distribution of next generation of genotypes is 16%, 48% and 36%. Successive proportions of the genotypes bb, bB, and BB after random matings are and the proportions settles down after one generation, as before, and the transmission probabilities of 0.4 and 0.6 remain constant. With these figures 16% of the population will have blue eyes and 48% + 36% = 84% will have brown eyes because B is dominant in the genotype bB.
10%, 60%, 30% → 16%, 48%, 36% → . . . → 16%, 48%, 36%
So the Hardy–Weinberg law implies that these proportions of genotypes bb, bB and BB will remain constant from generation to generation whatever the initial distribution of factors in the population. The dominant B gene does not take over and the proportions of genotypes are intrinsically stable.
Hardy stressed that his model was only approximate. Its simplicity and elegance depended on many assumptions which do not hold in real life. In the model the probability of gene mutation or changes in the genes themselves has been discounted, and the consequence of the transmission proportions being constant means it has nothing to say about evolution. In real life there is ‘genetic drift’ and the transmission probabilities of the factors do not stay constant. This will cause variations in the overall proportions and new species will evolve.
The Hardy–Weinberg law drew together Mendel’s theory – the ‘quantum theory’ of genetics – and Darwinism and natural selection in an intrinsic way. It awaited the genius of R.A. Fisher to reconcile the Mendelian theory of inheritance with the continuous theory where characteristics evolve.
What was missing in the science of genetics until the 1950s was a physical understanding of the genetic material itself. Then there was a dramatic advance contributed by Francis Crick, James Watson, Maurice Wilkins and Rosalind Franklin. The medium was deoxyribonucleic acid or DNA. Mathematics is needed to model the famous double helix (or a pair of spirals wrapped around a cylinder). The genes are located on segments of this double helix.
Mathematics is indispensable in studying genetics. From the basic geometry of the spirals of DNA and the potentially sophisticated Hardy–Weinberg law, mathematical models dealing with many characteristics (not just eye-colour) including male–female differences and also non-random mating have been developed. The science of genetics has also repaid the compliment to mathematics by suggesting new branches of abstract algebra of interest for their intriguing mathematical properties.
the condensed idea
Uncertainty in the gene pool

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















