

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Dimension
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
139-143
21-2-2016
2291
Leonardo da Vinci wrote in his notebook: ‘The science of painting begins with the point, then comes the line, the plane comes third, and the fourth the body in its vesture of planes.’ In da Vinci’s hierarchy, the point has dimension zero, the line is one-dimensional, the plane is two-dimensional and space is three-dimensional. What could be more obvious? It is the way the point, line, plane and solid geometry had been propagated by the Greek geometer Euclid, and Leonardo was following Euclid’s presentation.
That physical space is three-dimensional has been the view for millennia. In physical space we can move out of this page along the x-axis, or across it horizontally along the y-axis or vertically up the z-axis, or any combination of these. Relative to the origin (where the three axes meet) every point has a set of spatial coordinates specified by values of x, y and z and written in the form (x, y, z).
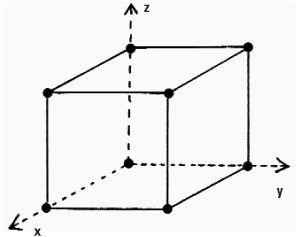
The space of three dimensions
A cube plainly has these three dimensions and so does everything else which has solidity. At school we are normally taught the geometry of the plane which is two-dimensional and we then move up to three dimensions – to ‘solid geometry’ – and stop there.
Around the beginning of the 19th century, mathematicians began to dabble in four dimensions and in even higher n-dimensional mathematics. Many philosophers and mathematicians began to ask whether higher dimensions existed.
Higher physical dimensions
Many leading mathematicians in the past thought that four dimensions could not be imagined. They queried the reality of four dimensions, and it became a challenge to explain this.
A common way to explain why four dimensions could be possible was to fall back to two dimensions. In 1884, an English schoolmaster and theologian, Edwin Abbott, published a highly popular book about ‘flatlanders’ who lived in the two-dimensional plane. They could not see triangles, squares or circles which existed in Flatland because they could not go out into the third dimension to view them. Their vision was severely limited. They had the same problems thinking about a third dimension that we do thinking of a fourth. But reading Abbott puts us into the frame of mind to accept the fourth dimension.
The need to contemplate the actual existence of a four-dimensional space became more urgent when Einstein came on the scene. Four-dimensional geometry became more plausible, and even understandable, because the extra dimension in Einstein’s model is time. Unlike Newton, Einstein conceived time as bound together with space in a four-dimensional space–time continuum. Einstein decreed that we live in a four-dimensional world with four coordinates (x, y, z, t) where t designates time.
Nowadays the four-dimensional Einsteinian world seems quite tame and matter of fact. A more recent model of physical reality is based on ‘strings’. In this theory, the familiar subatomic particles like electrons are the manifestations of extremely tiny vibrating strings. String theory suggests a replacement of the four-dimensional space–time continuum by a higher-dimensional version. Current research suggests that the dimension of the accommodating space–time continuum for string theory should be either 10, 11 or 26, depending on further assumptions and differing points of view.
A huge 2000 tonne magnet at CERN near Geneva, Switzerland, designed to engineer collisions of particles at high speeds, might help to resolve the issue. It is intended to uncover the structure of matter and, as a by-product, may point to a better theory and the ‘correct’ answer on dimensionality. The smart money seems to be that we’re living in an 11-dimensional universe.
Hyperspace
Unlike higher physical dimensions, there is absolutely no problem with a mathematical space of more than three dimensions. Mathematical space can be any number of dimensions. Since the early 19th century mathematicians have habitually used n variables in their work. George Green, a miller from Nottingham who explored the mathematics of electricity, and pure mathematicians A.L. Cauchy, Arthur Cayley and Hermann Grassmann, all described their mathematics in terms of n-dimensional hyperspace. There seemed no good reason to limit the mathematics and everything to be gained in elegance and clarity.
The idea behind n dimensions is merely an extension of three-dimensional coordinates (x, y, z) to an unspecified number of variables. A circle in two dimensions has an equation x2 + y2 = 1, a sphere in three dimensions has an equation x2 + y2 + z2 = 1, so why not a hypersphere in four dimensions with equation x2 + y2 + z2 + w2 = 1.
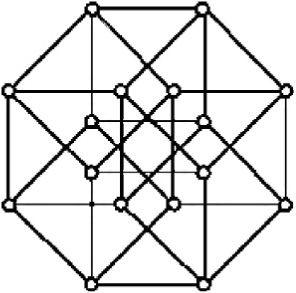
The four-dimensional cube
The eight corners of a cube in three dimensions have coordinates of the form (x, y, z) where each of the x, y, z are either 0 or 1. The cube has six faces each of which is a square and there are 2 × 2 × 2 = 8 corners. What about a four-dimensional cube? It will have coordinates of the form (x, y, z, w) where each of the x, y, z and w are either 0 or 1. So there are 2 × 2 × 2 × 2 = 16 possible corners for the four-dimensional cube, and eight faces, each of which is a cube. We cannot actually see this four-dimensional cube but we can create an artist’s impression of it on this sheet of paper. This shows a projection of the four-dimensional cube which exists in the mathematician’s imagination. The cubic faces can just about be perceived.
A mathematical space of many dimensions is quite a common occurrence for pure mathematicians. No claim is made for its actual existence though it may be assumed to exist in an ideal Platonic world. In the great problem of the classification of groups, for instance , the ‘monster group’ is a way of measuring symmetry in a mathematical space of 196,883 dimensions. We cannot ‘see’ this space in the same way as we can in the ordinary three-dimensional space, but it can still be imagined and dealt with in a precise way by modern algebra.
The mathematician’s concern for dimension is entirely separate from the meaning the physicist attaches to dimensional analysis. The common units of physics are measured in terms of mass M, length L, and time T. So, using their dimensional analysis a physicist can check whether equations make sense since both sides of an equation must have the same dimensions.
It is no good having force = velocity. A dimensional analysis gives velocity as metres per second so it has dimension of length divided by time or L/T, which we write as LT−1. Force is mass times acceleration, and as acceleration is metres per second per second, the net result is that force will have dimensions MLT−2.
Coordinated people
Human beings themselves are many dimensioned things. A human being has many more ‘coordinates’ than three. We could use (a, b, c, d, e, f, g, h), for age, height, weight, gender, shoe size, eye colour, hair colour, nationality, and so on. In place of geometrical points we might have people. If we limit ourselves to this eight-dimensional ‘space’ of people, John Doe might have coordinates like (43 years, 165 cm, 83 kg, male, 9, blue, blond, Danish) and Mary Smith’s coordinates might be (26 years, 157 cm, 56 kg, female, 4, brown, brunette, British).
Topology
Dimension theory is part of general topology. Other concepts of dimension can be defined independently in terms of abstract mathematical spaces. A major task is to show how they relate to each other. Leading figures in many branches of mathematics have delved into the meaning of dimension including Henri Lebesgue, L.E.J. Brouwer, Karl Menger, Paul Urysohn and Leopold Vietoris (until recently the oldest person in Austria, who died in 2002 aged 110).
The pivotal book on the subject was Dimension Theory. Published in 1948 by Witold Hurewicz and Henry Wallman – it is still seen as a watershed in our understanding of the concept of dimension.
Dimension in all its forms
From the three dimensions introduced by the Greeks the concept of dimension has been critically analysed and extended.
The n dimensions of mathematical space were introduced quite painlessly, while physicists have based theories on space–time (of dimension four) and recent versions of string theory which demand, 10, 11 and 26 dimensions. There have been forays into fractional dimensions with fractal shapes with several different measures being studied. Hilbert introduced an infinite-dimensional mathematical space that is now a basic framework for pure mathematicians. Dimension is so much more than the one, two, three of Euclidean geometry.
the condensed idea
Beyond the third dimension

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















