Word problems which are meant to be solved by algebra have been given to schoolchildren for centuries:

My niece Michelle is 6 years of age, and I am 40.
When will I be three times as old as her?

We could find this by a trial and error method but algebra is more economical. In x years from now Michelle will be 6 + x years and I will be 40 + x. I will be three times older than her when

  3 × (6 + x) = 40 + x

Multiply out the left-hand side of the equation and you’ll get 18 + 3x = 40 + x, and by moving all the xs over to one side of the equation and the numbers to the other, we find that 2x = 22 which means that x = 11. When I am 51 Michelle will be 17 years old. Magic!

What if we wanted to know when I will be twice as old as her? We can use the same approach, this time solving

   2 × (6 + x) = 40 + x

to get x = 28. She will be 34 when I am 68. All the equations above are of the simplest type – they are called ‘linear’ equations. They have no terms like x2 or x3, which make equations more difficult to solve. Equations with terms like x2 are called ‘quadratic’ and those with terms like x3 are called ‘cubic’ equations. In past times, x2 was represented as a square and because a square has four sides the term quadratic was used; x3 was represented by a cube.

Mathematics underwent a big change when it passed from the science of arithmetic to the science of symbols or algebra. To progress from numbers to letters is a mental jump but the effort is worthwhile.

The Italian connection

The theory of cubic equations was fully developed during the Renaissance. Unfortunately it resulted in an episode when mathematics was not always on its best behaviour. Scipione Del Ferro found the solution to the various specialized forms of the cubic equation and, hearing of it, Niccolò Fontana – dubbed ‘Tartaglia’ or ‘the stammerer’ – a teacher from Venice, published his own results on algebra but kept his methods secret. Girolamo Cardano from Milan persuaded Tartaglia to tell him of his methods but was sworn to secrecy. The method leaked out and a feud between the two developed when Tartaglia discovered his work had been published in Cardano’s 1545 book Ars Magna.

Origins

Algebra was a significant element in the work of Islamic scholars in the ninth century. Al-Khwarizmi wrote a mathematical textbook which contained the Arabic word al-jabr. Dealing with practical problems in terms of linear and quadratic equations, al-Khwarizmi’s ‘science of equations’ gave us the word ‘algebra’. Still later Omar Khayyam is famed for writing the Rubaiyat and the immortal lines (in translation)

A Jug of Wine, a Loaf of Bread – and Thou Beside me singing in the Wilderness

but in 1070, aged 22, he wrote a book on algebra in which he investigated the solution of cubic equations.

Girolamo Cardano’s great work on mathematics, published in 1545, was a watershed in the theory of equations for it contained a wealth of results on the cubic equation and the quartic equation – those involving a term of the kind x4. This flurry of research showed that the quadratic, cubic and quartic equations could all be solved by formulae involving only the operations +, –, ×, ÷, 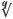(the last operation means the qth root). For example, the quadratic equation ax2 + bx + c = 0 can be solved using the formula:

If you want to solve the equation x2 – 3x + 2 = 0 all you do is feed the values a = 1, b = −3 and c = 2 into the formula.

The formulae for solving the cubic and quartic equations are long and unwieldy but they certainly exist. What puzzled mathematicians was that they could not produce a formula which was generally applicable to equations involving x5, the ‘quintic’ equations. What was so special about the power of five?

In 1826, the short-lived Niels Abel came up with a remarkable answer to this quintic equation conumdrum. He actually proved a negative concept, nearly always a more difficult task than proving that something can be done. Abel proved there could not be a formula for solving all quintic equations, and concluded that any further search for this particular holy grail would be futile. Abel convinced the top rung of mathematicians, but news took a long time to filter through to the wider mathematical world. Some mathematicians refused to accept the result, and well into the 19th century people were still publishing work which claimed to have found the non-existent formula.

The modern world

For 500 years algebra meant ‘the theory of equations’ but developments took a new turn in the 19th century. People realized that symbols in algebra could represent more than just numbers – they could represent ‘propositions’ and so algebra could be related to the study of logic. They could even represent higher-dimensional objects such as those found in matrix algebra . And, as many non-mathematicians have long suspected, they could even represent nothing at all and just be symbols moved about according to certain (formal) rules.

A significant event in modern algebra occurred in 1843 when the Irishman William Rowan Hamilton discovered the quaternions. Hamilton was seeking a system of symbols that would extend two-dimensional complex numbers to higher dimensions. For many years he tried three-dimensional symbols, but no satisfactory system resulted. When he came down for breakfast each morning his sons would ask him, ‘Well, Papa, can you multiply triplets?’ and he was bound to answer that he could only add and subtract them.

Success came rather unexpectedly. The three-dimensional quest was a dead end – he should have gone for four-dimensional symbols. This flash of inspiration came to him as he walked with his wife along the Royal Canal to Dublin. He was ecstatic about the sensation of discovery. Without hesitation, the 38-year-old vandal, Astronomer Royal of Ireland and Knight of the Realm, carved the defining relations into the stone on Brougham Bridge – a spot that is acknowledged today by a plaque. With the date scored into his mind, the subject became Hamilton’s obsession. He lectured on it year after year and published two heavyweight books on his ‘westward floating, mystic dream of four’.

One peculiarity of quarterions is that when they are multiplied together, the order in which this is done is vitally important, contrary to the rules of ordinary arithmetic. In 1844 the German linguist and mathematician Hermann Grassmann published another algebraic system with rather less drama. Ignored at the time, it has turned out to be far reaching. Today both quaternions and Grassmann’s algebra have applications in geometry, physics and computer graphics.

The abstract

In the 20th century the dominant paradigm of algebra was the axiomatic method. This had been used as a basis for geometry by Euclid but it wasn’t applied to algebra until comparatively recently.

Emmy Noether was the champion of the abstract method. In this modern algebra, the pervading idea is the study of structure where individual examples are subservient to the general abstract notion. If individual examples have the same structure but perhaps different notation they are called isomorphic.

The most fundamental algebraic structure is a group and this is defined by a list of axioms . There are structures with fewer axioms (such as groupoids, semi-groups and quasi-groups) and structures with more axioms (like rings, skew-fields, integral domains and fields). All these new words were imported into mathematics in the early 20th century as algebra transformed itself into an abstract science known as ‘modern algebra’.

the condensed idea

Solving for the unknown