


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-3-2022
Date: 4-3-2022
Date: 1-4-2022
|
Suppose a traveling salesman or tourist wants to visit the towns shown on a map.
They would wish to travel from one town to another, trying not to pass through any town twice on the trip, and usually they would wish to return to the starting point at the end of the trip. In terms of the underlying graph that represents the map, they would like to follow a cycle.
A cycle that passes through every vertex in a graph is called a Hamilton cycle and a graph with such a cycle is called Hamiltonian. The idea of such a spanning cycle was simultaneously developed by Hamilton in 1859 in a special case, and more generally by Kirkman in 1856.
A Hamilton path is a path that passes through every vertex. If you have a Hamilton cycle, you can construct a Hamilton path by deleting any one edge.
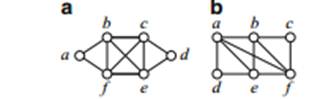
Fig. 1.1 Two sample graphs for discussing Hamilton cycles
Sample Problem 1.1 Consider the graph in Fig. 1.1a. Which of the following are Hamilton cycles?
(i) (a,b,e,d,c, f,a) (ii) (a,b,e,c,d,e, f,a)
(iii) (a,b,c,d,e, f,a) (iv) (a,b,c,e, f,a)
Solution. (i) and (iii) are Hamiltonian. (ii) is not; it contains a repeat of e. (iv) is not; vertex d is omitted.
At first, the problem of deciding whether a graph is Hamiltonian sounds similar to the problem of Euler circuits. However, the two problems are strikingly different in one regard. We found a very easy test for the Eulerian property, but no nice necessary and sufficient conditions are known for the existence of Hamilton cycles.
It is easy to see that the complete graphs with three or more vertices are Hamiltonian, and any ordering of the vertices gives a Hamilton cycle. We can discuss Hamiltonicity in a number of other particular cases, but there are no known theorems that characterize Hamiltonian graphs.
Suppose you want to find all Hamilton cycles in a graph with v vertices. Your first instinct might be to list all possible arrangements of v vertices and then delete those with two consecutive vertices that are not adjacent in the graph. This process can then be made more efficient by observing that the v lists a1a2 ...av−1av, a2a3 ... ava1, ..., and ava1 ...av−2av−1 all represent the same cycle (written with a different starting point), and also avav−1 ...a2a1 is the same Hamilton cycle as a1a2 ...av−1av (traversed in the opposite direction).
Another shortcut is available. If there is a vertex of degree 2, then any Hamilton cycle must contain the two edges touching it. If x has degree 2, and suppose its two neighbors are y and z, then xy and xz are in every Hamilton cycle. So it suffices to delete x, add an edge yz, find all Hamilton cycles in the new graph, and delete any that do not contain the edge yz. The Hamilton cycles in the original graph are then formed by inserting x between y and z.
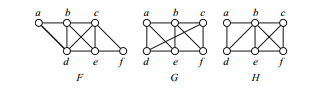
Fig. 1.2 Find all Hamilton cycles
Sample Problem 1.2 Find all Hamilton cycles in the graph F of Fig. 1.2.
Solution. The graph F has two vertices of degree 2, namely a and f . When we replace these vertices by edges bd and ce, we obtain the complete graph with vertices a,b,c,d (multiple edges can be ignored). This complete graph has three Hamilton cycles: there are six arrangements starting with b, namely bcde, bced, bdce, bedc, bdec, becd, and the latter three are just the former three written in reverse. bcde yields a cycle that does not contain edges bd and ce. The other two give the cycles bc f eda and badc f e, so these are the two Hamilton cycles in F.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|