We shall now bring our discussion of waves to a close with a few general remarks about the wave equation. These remarks are intended to give some view of the future—not that we can understand everything exactly just now, but rather to see what things are going to look like when we study waves a little more. First of all, the wave equation for sound in one dimension was

where c is the speed of whatever the wave is—in the case of sound, it is the sound speed; in the case of light, it is the speed of light. We showed that for a sound wave the displacements would propagate themselves at a certain speed. But the excess pressure also propagates at a certain speed, and so does the excess density. So we should expect that the pressure would satisfy the same equation, as indeed it does. We shall leave it to the reader to prove that it does. Hint: ρ_e is proportional to the rate of change of χ with respect to x. Therefore, if we differentiate the wave equation with respect to x, we will immediately discover that ∂χ/∂x satisfies the same equation. That is to say, ρ_e satisfies the same equation. But P_e is proportional to ρ_e, and therefore P_e does too. So, the pressure, the displacements, everything, satisfy the same wave equation.

Usually, one sees the wave equation for sound written in terms of pressure instead of in terms of displacement, because the pressure is a scalar and has no direction. But the displacement is a vector and has direction, and it is thus easier to analyze the pressure.

The next matter we discuss has to do with the wave equation in three dimensions. We know that the sound wave solution in one dimension is e^i(ωt−kx), with ω=kc_s, but we also know that in three dimensions a wave would be represented by e^{i(ωt−k_xx−kyy−k_zz)}, where, in this case, ω²=k²c²_s, which is, of course, (k²_x+k²_y+k²_z)c²_s. Now what we want to do is to guess what the correct wave equation in three dimensions is. Naturally, for the case of sound this can be deduced by going through the same dynamic argument in three dimensions that we made in one dimension. But we shall not do that; instead we just write down what comes out: the equation for the pressure (or displacement, or anythinAg) is

That this is true can be verified by substituting in e^{i(ωt−k⋅r)}. Clearly, every time we differentiate with respect to x, we multiply by −ikx. If we differentiate twice, it is equivalent to multiplying by −k²_x, so the first term would become −k²_xP_e, for that wave. Similarly, the second term becomes −k²_yP_e, and the third term becomes −k²_zP_e. On the right, we get −(ω²/c²_s)P_e. Then, if we take away the P_e’s and change the sign, we see that the relationship between k and ω is the one that we want.

Working backwards again, we cannot resist writing down the grand equation which corresponds to the dispersion equation (48.22) for quantum-mechanical waves. If ϕ represents the amplitude for finding a particle at position x,y,z, at the time t, then the great equation of quantum mechanics for free particles is this:

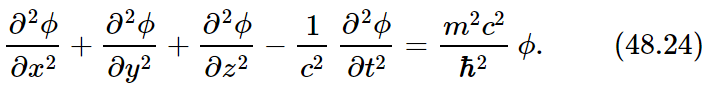
First of all, the relativity character of this expression is suggested by the appearance of x, y, z and t in the nice combination relativity usually involves. Second, it is a wave equation which, if we try a plane wave, would produce as a consequence that −k²+ω²/c²=m²c²/ℏ², which is the right relationship for quantum mechanics. There is still another great thing contained in the wave equation: the fact that any superposition of waves is also a solution. So this equation contains all of the quantum mechanics and the relativity that we have been discussing so far, at least so long as it deals with a single particle in empty space with no external potentials or forces on it!