Now the wave number is the rate of change of phase with distance, and the frequency is the rate of change of phase with time, and in these expressions, we see a close analogy with the Lorentz transformation of the position and time: if ω is thought of as being like t, and k is thought of as being like x divided by c², then the new ω′ will be like t′, and the new k′ will be like x′/c². That is to say, under the Lorentz transformation ω and k transform the same way as do t and x. They constitute what we call a four-vector; when a quantity has four components transforming like time and space, it is a four-vector. Everything seems all right, then, except for one little thing: we said that a four-vector has to have four components; where are the other two components? We have seen that ω and k are like time and space in one space direction, but not in all directions, and so we must next study the problem of the propagation of light in three space dimensions, not just in one direction, as we have been doing up until now.

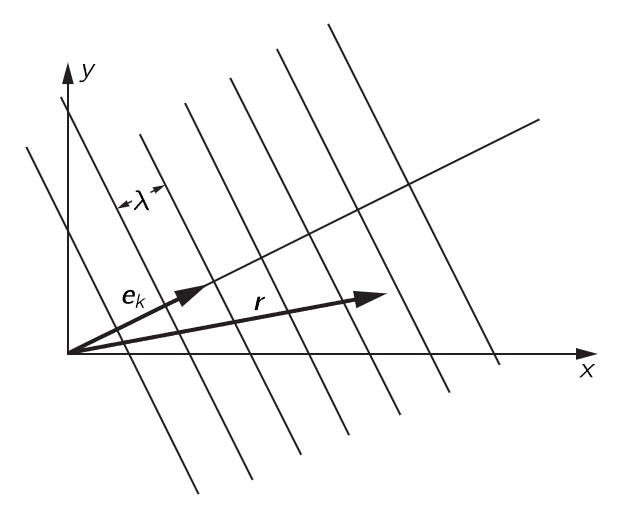
Fig. 34–11. A plane wave travelling in an oblique direction.

Suppose that we have a coordinate system, x, y, z, and a wave which is travelling along and whose wavefronts are as shown in Fig. 34–11. The wavelength of the wave is λ, but the direction of motion of the wave does not happen to be in the direction of one of the axes. What is the formula for such a wave? The answer is clearly cos(ωt−ks), where k=2π/λ and s is the distance along the direction of motion of the wave—the component of the spatial position in the direction of motion. Let us put it this way: if r is the vector position of a point in space, then s is r⋅e_k, where e_k is a unit vector in the direction of motion. That is, s is just rcos(r,e_k), the component of distance in the direction of motion. Therefore, our wave is cos(ωt−ke_k⋅r).

Now it turns out to be very convenient to define a vector k, which is called the wave vector, which has a magnitude equal to the wave number, 2π/λ, and is pointed in the direction of propagation of the waves:

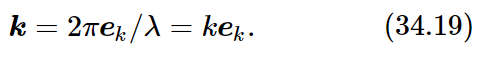
Using this vector, our wave can be written as cos(ωt−k⋅r), or as cos(ωt−k_xx−k_yy−k_zz). What is the significance of a component of k, say k_x? Clearly, k_x is the rate of change of phase with respect to x. Referring to Fig. 34–11, we see that the phase changes as we change x, just as if there were a wave along x, but of a longer wavelength. The “wavelength in the x-direction” is longer than a natural, true wavelength by the secant of the angle α between the actual direction of propagation and the x-axis:

Therefore the rate of change of phase, which is proportional to the reciprocal of λ_x, is smaller by the factor cosα; that is just how k_x would vary—it would be the magnitude of k, times the cosine of the angle between k and the x-axis!

That, then, is the nature of the wave vector that we use to represent a wave in three dimensions. The four quantities ω, k_x, k_y, k_z transform in relativity as a four-vector, where ω corresponds to the time, and k_x, k_y, k_z correspond to the x-, y-, and z-components of the four-vector.

There are ways of making relativistic dot products with four-vectors. If we use the position vector x_μ, where μ stands for the four components (time and three space ones), and if we call the wave vector k_μ, where the index μ again has four values, time and three space ones, then the dot product of x_μ and k_μ is written ∑′k_μx_μ. This dot product is an invariant, independent of the coordinate system; what is it equal to? By the definition of this dot product in four dimensions, it is

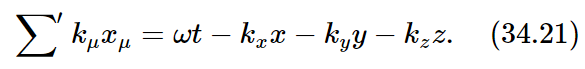
We know from our study of vectors that ∑′k_μx_μ is invariant under the Lorentz transformation, since k_μ is a four-vector. But this quantity is precisely what appears inside the cosine for a plane wave, and it ought to be invariant under a Lorentz transformation. We cannot have a formula with something that changes inside the cosine, since we know that the phase of the wave cannot change when we change the coordinate system.