معادلة العدسة الرقيقة

يعتبر رسم الأشعة، أسلوباً مقيداً لتخطيط العلاقة بين الصورة والجسم. إلا أننا نود أن نطرح وسيلة تحليلية لتناول مفيداً لتناول هذه العلاقة. وسنبدأ هذه العملية بدراسة الصورة المتكونة بواسطة العدسة المبين في الشكل 1)). المثلثان. ABH و EBD في الشكل (أ) متشابهان ولذا يمكننا أن نكتب الآتي:

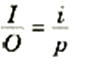
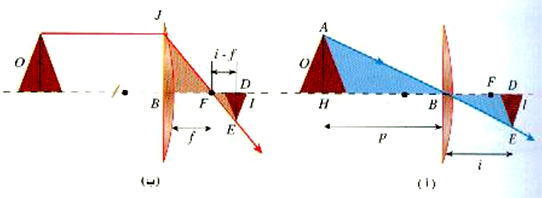
الشكل 1)): المثلثان ABH و EBD متشابهان وكذلك المثلثان JFB و EDF.

وقد استخدمنا نفس الرموز لعد الجسم وبعد الصورة مثلما فعلنا في حالة المرايا. ومن المثلثين المتشابهين JFB و EDF في الجزء (ب) نحصل على :

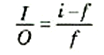
وبمساواة المعادلتين وإجراء بعض الاختصارات:

(1)                      

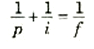
هذه العلاقة هي نفس معادلة المرايا بالضبط ولذلك أعطيناها نفس الرقم. وقد اعتبرنا p موجباً بالنسبة لجسم أمام العدسة واعتبرنا i موجباً بالنسبة للصورة الحقيقية المتكونة خلف العدسة.

أما بالنسبة للعدسات المفرقة فيمكننا اشتقاق العلاقة بالإشارة إلى مجموعات المثلثات المتشابهة في الشكل 2)). ونجد عندئذ

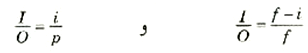
وبمساواة هاتين المعادلتين وإجراء الاختصارات نجد أن

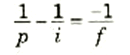
ونستطيع جعل هذه المعادلة متطابقة مع المعادلة 1)) إذا اتفقنا على قاعدة الإشارات المستخدمة لكل من f و p و i: 

لكي نستخدم المعادلة (1) لجميع مواقف العدسات.

1ـ بعد الجسم P موجب إذا كان الجسم أمام العدسة وسالبة إذا كان خلفها (سوف نتناول القيم السالبة لبعد الجسم في القسم التالي).

2- بعد الصورة i موجب إذا تكونت الصورة  خلف العدسة (صورة حقيقية) وسالب إذا تكونت الصورة أمام العدسة( صورة تقديرية).

3- البعد البؤري موجب بالنسبة لعدسة مجمعة وسالب لعدسة مفرقة.

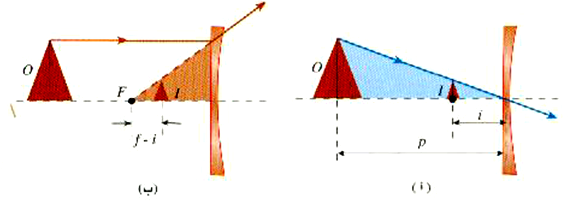
الشكل 2)): إن أخذ المثلثان المتشابهة في الاعتبار، يؤدي إلى معادلة الرقيقة بالنسبة للعدسات المفرقة.

ونستطيع بمساعدة قاعدة الإشارات أن نضع تعريفاً للتكبير كما فعلنا مع المرايا:

(2)                 

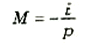
ومرة أخرى، تتيح الإشارة السالبة لنا أن نحدد الصور المقلوبة على أنها ذات القيم السالبة للتكبير M والصور المعتدلة ستكون M موجبة بالنسبة لها.

والمشاهدات العامة التالية ذات فائدة عند تناول مسائل العدسات:

1ـ  تكون العدسات المفرقة دائماً صوراً تقديرية معتدلة ومصغرة إذا كان الجسم حقيقياً مهما كان موقع الجسم أمام العدسة.

مواضيع ذات صلة

Mirror reflections

The sensation of color

Physiochemistry of color vision

The mechanism of color vision

The chromaticity diagram

Measuring the color sensation

Color depends on intensity

Aberration

The ω,k four-vector

Moving sources

Anomalous refraction

The intensity of reflected light