
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Resolving power of a grating
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 30
2024-03-20
1318
We are now in a position to understand a number of interesting phenomena. For example, consider the use of a grating for separating wavelengths. We noticed that the whole spectrum was spread out on the screen, so a grating can be used as an instrument for separating light into its different wavelengths. One of the interesting questions is: supposing that there were two sources of slightly different frequency, or slightly different wavelength, how close together in wavelength could they be such that the grating would be unable to tell that there were really two different wavelengths there? The red and the blue were clearly separated. But when one wave is red and the other is slightly redder, very close, how close can they be? This is called the resolving power of the grating, and one way of analyzing the problem is as follows. Suppose that for light of a certain color we happen to have the maximum of the diffracted beam occurring at a certain angle. If we vary the wavelength the phase 2πd sin θ/λ is different, so of course the maximum occurs at a different angle. That is why the red and blue are spread out. How different in angle must it be in order for us to be able to see it? If the two maxima are exactly on top of each other, of course we cannot see them. If the maximum of one is far enough away from the other, then we can see that there is a double bump in the distribution of light. In order to be able to just make out the double bump, the following simple criterion, called Rayleigh’s criterion, is usually used (Fig. 30–6). It is that the first minimum from one bump should sit at the maximum of the other. Now it is very easy to calculate, when one minimum sits on the other maximum, how much the difference in wavelength is. The best way to do it is geometrically.
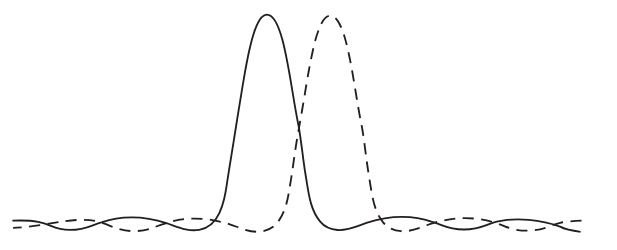
Fig. 30–6. Illustration of the Rayleigh criterion. The maximum of one pattern falls on the first minimum of the other.
In order to have a maximum for wavelength λ′, the distance Δ (Fig. 30–3) must be nλ′, and if we are looking at the mth-order beam, it is mnλ′. In other words, 2πd sin θ/λ′=2πm, so nd sin θ, which is Δ, is mλ′ times n, or mnλ′. For the other beam, of wavelength λ, we want to have a minimum at this angle. That is, we want Δ to be exactly one wavelength λ more than mnλ. That is, Δ=mnλ+λ=mnλ′. Thus, if λ′=λ+Δλ, we find

The ratio λ/Δλ is called the resolving power of a grating; we see that it is equal to the total number of lines in the grating, times the order. It is not hard to prove that this formula is equivalent to the formula that the error in frequency is equal to the reciprocal time difference between extreme paths that are allowed to interfere:1
Δν = 1/T.
In fact, that is the best way to remember it, because the general formula works not only for gratings, but for any other instrument whatsoever, while the special formula (30.9) depends on the fact that we are using a grating.
_______________________________________________________________
Margin
1- In our case T=Δ/c=mnλ/c, where c is the speed of light. The frequency ν=c/λ, so Δν= cΔλ/λ2.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















