In technical work with antennas and wires it is possible to arrange that all the phases of the little oscillators, or antennas, are equal. The question is whether and how we can do a similar thing with light. We cannot at the present time literally make little optical-frequency radio stations and hook them up with infinitesimal wires and drive them all with a given phase. But there is a very easy way to do what amounts to the same thing.

Suppose that we had a lot of parallel wires, equally spaced at a spacing d, and a radiofrequency source very far away, practically at infinity, which is generating an electric field which arrives at each one of the wires at the same phase (it is so far away that the time delay is the same for all of the wires). (One can work out cases with curved arrays, but let us take a plane one.) Then the external electric field will drive the electrons up and down in each wire. That is, the field which is coming from the original source will shake the electrons up and down, and in moving, these represent new generators. This phenomenon is called scattering: a light wave from some source can induce a motion of the electrons in a piece of material, and these motions generate their own waves. Therefore, all that is necessary is to set up a lot of wires, equally spaced, drive them with a radiofrequency source far away, and we have the situation that we want, without a whole lot of special wiring. If the incidence is normal, the phases will be equal, and we will get exactly the circumstance we have been discussing. Therefore, if the wire spacing is greater than the wavelength, we will get a strong intensity of scattering in the normal direction, and in certain other directions given by (30.6).

This can also be done with light! Instead of wires, we use a flat piece of glass and make notches in it such that each of the notches scatters a little differently than the rest of the glass. If we then shine light on the glass, each one of the notches will represent a source, and if we space the lines very finely, but not closer than a wavelength (which is technically almost impossible anyway), then we would expect a miraculous phenomenon: the light not only will pass straight through, but there will also be a strong beam at a finite angle, depending on the spacing of the notches! Such objects have actually been made and are in common use—they are called diffraction gratings.

In one of its forms, a diffraction grating consists of nothing but a plane glass sheet, transparent and colorless, with scratches on it. There are often several hundred scratches to the millimeter, very carefully arranged so as to be equally spaced. The effect of such a grating can be seen by arranging a projector so as to throw a narrow, vertical line of light (the image of a slit) onto a screen. When we put the grating into the beam, with its scratches vertical, we see that the line is still there but, in addition, on each side we have another strong patch of light which is colored. This, of course, is the slit image spread out over a wide angular range, because the angle θ in (30.6) depends upon λ, and lights of different colors, as we know, correspond to different frequencies, and therefore different wavelengths. The longest visible wavelength is red, and since d sin θ=λ, that requires a larger θ. And we do, in fact, find that red is at a greater angle out from the central image! There should also be a beam on the other side, and indeed we see one on the screen. Then, there might be another solution of (30.6) when m=2. We do see that there is something vaguely there—very weak—and there are even other beams beyond.

We have just argued that all these beams ought to be of the same strength, but we see that they actually are not and, in fact, not even the first ones on the right and left are equal! The reason is that the grating has been carefully built to do just this. How? If the grating consists of very fine notches, infinitesimally wide, spaced evenly, then all the intensities would indeed be equal. But, as a matter of fact, although we have taken the simplest case, we could also have considered an array of pairs of antennas, in which each member of the pair has a certain strength and some relative phase. In this case, it is possible to get intensities which are different in the different orders. A grating is often made with little “sawtooth” cuts instead of little symmetrical notches. By carefully arranging the “sawteeth,” more light may be sent into one particular order of spectrum than into the others. In a practical grating, we would like to have as much light as possible in one of the orders. This may seem a complicated point to bring in, but it is a very clever thing to do, because it makes the grating more useful.

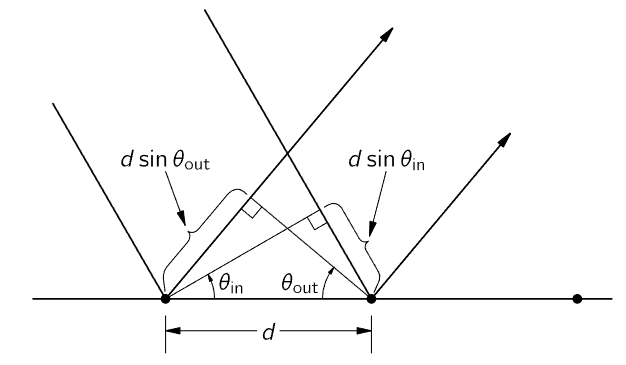
Fig. 30–4. The path difference for rays scattered from adjacent rulings of a grating is d sin θ_out−d sin θ_in.

So far, we have taken the case where all the phases of the sources are equal. But we also have a formula for ϕ when the phases differ from one to the next by an angle α. That requires wiring up our antennas with a slight phase shift between each one. Can we do that with light? Yes, we can do it very easily, for suppose that there was a source of light at infinity, at an angle such that the light is coming in at an angle θ_in, and let us say that we wish to discuss the scattered beam, which is leaving at an angle θ_out (Fig. 30–4). The θ_out is the same θ as we have had before, but the θ_in is merely a means for arranging that the phase of each source is different: the light coming from the distant driving source first hits one scratch, then the next, then the next, and so on, with a phase shift from one to the other, which, as we see, is α=−2πd sin θ_in/λ. Therefore, we have the formula for a grating in which light both comes in and goes out at an angle:

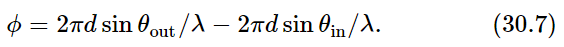
Let us try to find out where we get strong intensity in these circumstances. The condition for strong intensities is, of course, that ϕ should be a multiple of 2π. There are several interesting points to be noted.

One case of rather great interest is that which corresponds to m=0, where d is less than λ/2; in fact, this is the only solution. In this case we see that sin θ_out=sin θ_in, which may mean that θ_out is the supplement of θ_in so the light comes out in the same direction as the light which was exciting the grating. We might think that the light “goes right through.” No, it is different light that we are talking about. The light that goes right through is from the original source; what we are talking about is the new light which is generated by scattering. It turns out that the scattered light is going in the same direction as the original light, in fact it can interfere with it—a feature which we will study later.

There is another solution for this same case: θ_out may equal θ_in. So not only do we get a beam in the same direction as the incoming beam but also one in another direction, such that the angle of incidence is equal to the angle of scattering. This we call the reflected beam.

So, we begin to understand the basic machinery of reflection: the light that comes in generates motions of the atoms in the reflector, and the reflector then regenerates a new wave, and one of the solutions for the direction of scattering, the only solution if the spacing of the scatterers is small compared with one wavelength, is that the angle at which the light comes out is equal to the angle at which it comes in!

Next, we discuss the special case when d→0. That is, we have just a solid piece of material, so to speak, but of finite length. In addition, we want the phase shift from one scatterer to the next to go to zero. In other words, we put more and more antennas between the other ones, so that each of the phase differences is getting smaller, but the number of antennas is increasing in such a way that the total phase difference, between one end of the line and the other, is constant. Let us see what happens to (30.3) if we keep the difference in phase nϕ from one end to the other constant (say nϕ=Φ), letting the number go to infinity and the phase shift ϕ of each one go to zero. But now ϕ is so small that sin ϕ=ϕ, and if we also recognize n²I₀ as I_m, the maximum intensity at the center of the beam, we find

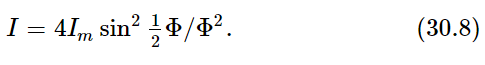
This limiting case is what is shown in Fig. 30–2.

In such circumstances we find the same general kind of a picture as for finite spacing with d<λ/2; all the side lobes are practically the same as before, but there are no subsidiary higher-order maxima. If the scatterers are all in phase, we get a maximum in the direction θ_out=0, and a minimum when the distance Δ is equal to λ, just as for finite d and n. So we can even analyze a continuous distribution of scatterers or oscillators, by using integrals instead of summing.

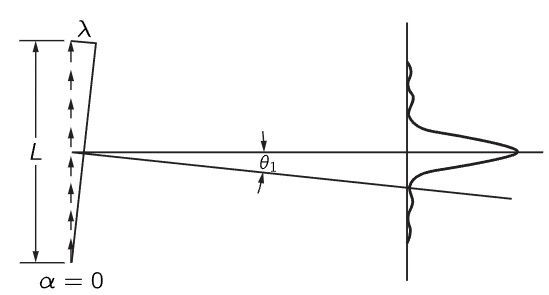
Fig. 30–5. The intensity pattern of a continuous line of oscillators has a single strong maximum and many weak “side lobes.”

As an example, suppose there were a long line of oscillators, with the charge oscillating along the direction of the line (Fig. 30–5). From such an array the greatest intensity is perpendicular to the line. There is a little bit of intensity up and down from the equatorial plane, but it is very slight. With this result, we can handle a more complicated situation. Suppose we have a set of such lines, each producing a beam only in a plane perpendicular to the line. To find the intensity in various directions from a series of long wires, instead of infinitesimal wires, is the same problem as it was for infinitesimal wires, so long as we are in the central plane perpendicular to the wires; we just add the contribution from each of the long wires. That is why, although we actually analyzed only tiny antennas, we might as well have used a grating with long, narrow slots. Each of the long slots produces an effect only in its own direction, not up and down, but they are all set next to each other horizontally, so they produce interference that way.

Thus, we can build up more complicated situations by having various distributions of scatterers in lines, planes, or in space. The first thing we did was to consider scatterers in a line, and we have just extended the analysis to strips; we can work it out by just doing the necessary summations, adding the contributions from the individual scatterers. The principle is always the same.