
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Resolving power
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 27
2024-03-18
1221
Another interesting question—a very important technical question with all optical instruments—is how much resolving power they have. If we build a microscope, we want to see the objects that we are looking at. That means, for instance, that if we are looking at a bacterium with a spot on each end, we want to see that there are two dots when we magnify them. One might think that all we have to do is to get enough magnification—we can always add another lens, and we can always magnify again and again, and with the cleverness of designers, all the spherical aberrations and chromatic aberrations can be cancelled out, and there is no reason why we cannot keep on magnifying the image. So the limitations of a microscope are not that it is impossible to build a lens that magnifies more than 2000 diameters. We can build a system of lenses that magnifies 10,000 diameters, but we still could not see two points that are too close together because of the limitations of geometrical optics, because of the fact that least time is not precise.
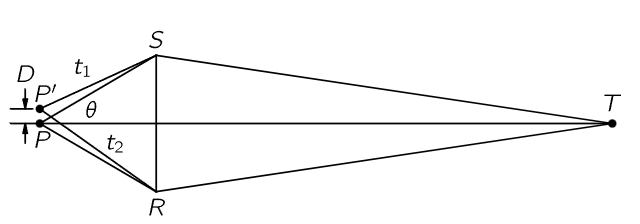
Fig. 27–9. The resolving power of an optical system.
To discover the rule that determines how far apart two points have to be so that at the image they appear as separate points can be stated in a very beautiful way associated with the time it takes for different rays. Suppose that we disregard the aberrations now, and imagine that for a particular point P (Fig. 27–9) all the rays from object to image T take exactly the same time. (It is not true, because it is not a perfect system, but that is another problem.) Now take another nearby point, P′, and ask whether its image will be distinct from T. In other words, whether we can make out the difference between them. Of course, according to geometrical optics, there should be two point images, but what we see may be rather smeared and we may not be able to make out that there are two points. The condition that the second point is focused in a distinctly different place from the first one is that the two times for the extreme rays P′ST and P′RT on each side of the big opening of the lenses to go from one end to the other, must not be equal from the two possible object points to a given image point. Why? Because, if the times were equal, of course both would focus at the same point. So the times are not going to be equal. But by how much do they have to differ so that we can say that both do not come to a common focus, so that we can distinguish the two image points? The general rule for the resolution of any optical instrument is this: two different point sources can be resolved only if one source is focused at such a point that the times for the maximal rays from the other source to reach that point, as compared with its own true image point, differ by more than one period. It is necessary that the difference in time between the top ray and the bottom ray to the wrong focus shall exceed a certain amount, namely, approximately the period of oscillation of the light:

where ν is the frequency of the light (number of oscillations per second; also speed divided by wavelength). If the distance of separation of the two points is called D, and if the opening half-angle of the lens is called θ, then one can demonstrate that (27.17) is exactly equivalent to the statement that D must exceed λ/2nsinθ, where n is the index of refraction at P and λ is the wavelength. The smallest things that we can see are therefore approximately the wavelength of light. A corresponding formula exists for telescopes, which tells us the smallest difference in angle between two stars that can just be distinguished.1
________________________________________________________
Margin
1- The angle is about λ/D, where D is the lens diameter. Can you see why?
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















