The ideas of probability are certainly useful in describing the behavior of the 10²² or so molecules in a sample of a gas, for it is clearly impractical even to attempt to write down the position or velocity of each molecule. When probability was first applied to such problems, it was considered to be a convenience—a way of dealing with very complex situations. We now believe that the ideas of probability are essential to a description of atomic happenings. According to quantum mechanics, the mathematical theory of particles, there is always some uncertainty in the specification of positions and velocities. We can, at best, say that there is a certain probability that any particle will have a position near some coordinate x.

We can give a probability density p₁(x), such that p₁(x)Δx is the probability that the particle will be found between x and x+Δx. If the particle is reasonably well localized, say near x₀, the function p₁(x) might be given by the graph of Fig. 6–10 (a). Similarly, we must specify the velocity of the particle by means of a probability density p₂(v), with p₂(v) Δv the probability that the velocity will be found between v and v+Δv.

Fig. 6–10. Probability densities for observation of the position and velocity of a particle.

It is one of the fundamental results of quantum mechanics that the two functions p₁(x) and p₂(v) cannot be chosen independently and, in particular, cannot both be made arbitrarily narrow. If we call the typical “width” of the p₁(x) curve [Δx], and that of the p₂(v) curve [Δv] (as shown in the figure), nature demands that the product of the two widths be at least as big as the number ℏ/2m, where m is the mass of the particle. We may write this basic relationship as

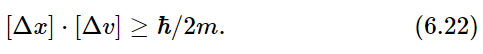
This equation is a statement of the Heisenberg uncertainty principle that we mentioned earlier.

Since the right-hand side of Eq. (6.22) is a constant, this equation says that if we try to “pin down” a particle by forcing it to be at a particular place, it ends up by having a high speed. Or if we try to force it to go very slowly, or at a precise velocity, it “spreads out” so that we do not know very well just where it is. Particles behave in a funny way!

The uncertainty principle describes an inherent fuzziness that must exist in any attempt to describe nature. Our most precise description of nature must be in terms of probabilities. There are some people who do not like this way of describing nature. They feel somehow that if they could only tell what is really going on with a particle, they could know its speed and position simultaneously. In the early days of the development of quantum mechanics, Einstein was quite worried about this problem. He used to shake his head and say, “But, surely God does not throw dice in determining how electrons should go!” He worried about that problem for a long time and he probably never really reconciled himself to the fact that this is the best description of nature that one can give. There are still one or two physicists who are working on the problem who have an intuitive conviction that it is possible somehow to describe the world in a different way and that all of this uncertainty about the way things are can be removed. No one has yet been successful.

The necessary uncertainty in our specification of the position of a particle becomes most important when we wish to describe the structure of atoms. In the hydrogen atom, which has a nucleus of one proton with one electron outside of the nucleus, the uncertainty in the position of the electron is as large as the atom itself! We cannot, therefore, properly speak of the electron moving in some “orbit” around the proton. The most we can say is that there is a certain chance p(r)ΔV, of observing the electron in an element of volume ΔV at the distance r from the proton. The probability density p(r) is given by quantum mechanics. For an undisturbed hydrogen atom p(r)=Ae^−2r/a. The number a is the “typical” radius, where the function is decreasing rapidly. Since there is a small probability of finding the electron at distances from the nucleus much greater than a, we may think of a as “the radius of the atom,” about 10⁻¹⁰ meter.

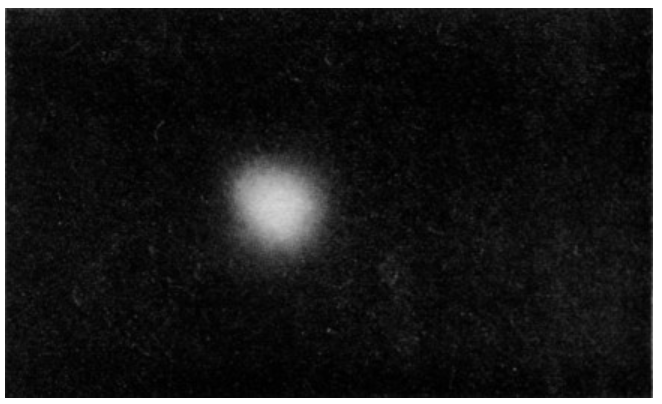
Fig. 6–11. A way of visualizing a hydrogen atom. The density (whiteness) of the cloud represents the probability density for observing the electron.

We can form an image of the hydrogen atom by imagining a “cloud” whose density is proportional to the probability density for observing the electron. A sample of such a cloud is shown in Fig. 6–11. Thus our best “picture” of a hydrogen atom is a nucleus surrounded by an “electron cloud” (although we really mean a “probability cloud”). The electron is there somewhere, but nature permits us to know only the chance of finding it at any particular place.

In its efforts to learn as much as possible about nature, modern physics has found that certain things can never be “known” with certainty. Much of our knowledge must always remain uncertain. The most we can know is in terms of probabilities.