
حالات خاصة(الدوال كثيرة الحدود) : SPECIAL CARES
 المؤلف:
د.لحسن عبدالله باشيوة
المؤلف:
د.لحسن عبدالله باشيوة
 المصدر:
الرياضيات الاساسية وتطبيقاتها
المصدر:
الرياضيات الاساسية وتطبيقاتها
 الجزء والصفحة:
21-24
الجزء والصفحة:
21-24
 31-10-2021
31-10-2021
 3553
3553
حالات خاصة : SPECIAL CARES
الدوال الثابت كثير حدود من الدرجة صفر :
Zero dagree polynomial function
هي كثير حدود صيغتها العامة من الشكل :
f(x) = a
حيث إن : a عدد حقيقي ثابت.
مثال : f(x) = 1000000 ، يمكن اعتبار كل دالة تساوي أي عدد من الأعداد الحقيقية هي كثيرات حدود من الدرجة صفر.
كثير حدود من الدرجة الأولى : polynomial Function of The First Degree
هي دالة خطية (كثير حدود من الدرجة الاولى) ، وصيغتها العامة من الشكل :
F(x) = a x + b
وهي تمثل كل معادلات المستقيمات في المستوى الديكارتي (X,Y). وتمتاز بعض هذه الدوال بالخاصية الخطية، وهي بالتعبير الرياضي تحقق الشرط :
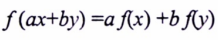
لكل قيم المتغيرين xy والثوابت a,b ، تمثل المعادلة y = ax + b في المستوى (X,Y) معادلة المستقيم الذي ميله a ، ويتقاطع مع المحور OY في النقطة (0 , b)، ويمكن إيجاد العددين الحقيقيين b , a من خلال بعض المعطيات الجاهزة أهمها :
1- معرفة نقطتين يمر عليهما المستقيم (x2 , y2) , (x1 , y1) :

شكل (1-1)
2- المستقيم يمر بالنقطة (x2 , y2) ويوازي المستقيم الذي معادلته  إذن عناصر المستقيم هي : b = y2 – ax2 , a = a*.
إذن عناصر المستقيم هي : b = y2 – ax2 , a = a*.
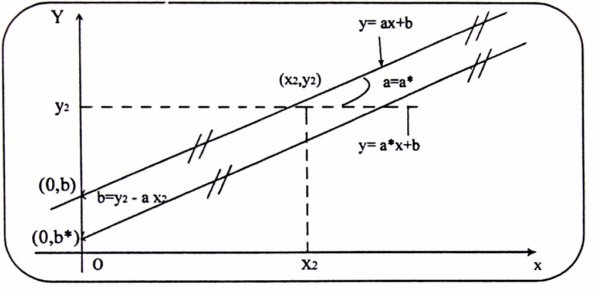
شكل (1-2)
3- المستقيم يمر بالنقطة (x1 , y1) ويعامد المستقيم الذي معادلته 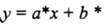 إذن عناصر المستقيم هي :
إذن عناصر المستقيم هي : 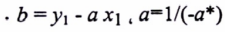
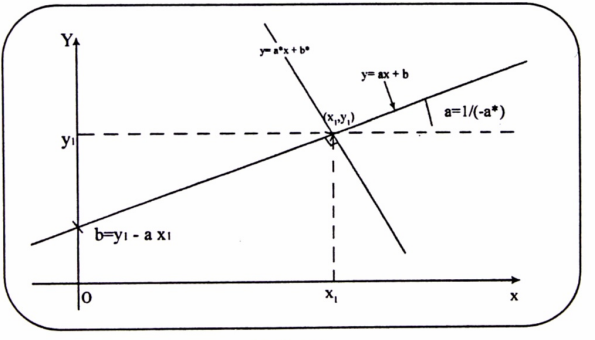
شكل (1-3)
4- حالات أخرى خاصة تتمثل في حالة المستقيم يوازي أو يعامد أو يعامد كلاً من محور OX أو محور OY.
تمرين : أوجد معادلة المستقيم في الحالات التالية :
1- المستقيم المار بالنقطتين N(2,6) ، M(-1,5).
2- المستقيم الذي يقطع المحور الصادي في 6 ، ويقطع المحور السيني في 5-.
3- المستقيم المار بالنقطة (2,3) وميله مالا نهاية (∞).
4- المستقيم المار بالنقطة N(2,6) ، ويوازي المستقيم الذي معادلته 3y + 2x = 5
5- المستقيم المار بالنقطة M(-1,5) ، ويعامد المستقيم الذي معادلته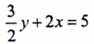
2- كثير حدود من الدرجة الثانية :
Polynomial Function of the 2nd Degree
هي الة من الدرجة التربيعية (كثير حدود من الدرجة الثانية) صيغتها العامة من الشكل :

حيث إن : a, b, c ثوابت حقيقية.
3- كثير حدود من الدرجة الثالثة :
Polynomial Function of the Third Degree
هي كثير حدود صبغتها العامة من الشكل :

حيث إن a, b, , c, d ثوابت حقيقية.
4- كثير حدود من الدرجة الرابعة :
Polynomial Function of the Fourth Degree
هي كثير حدود صيغتها العامة من الشكل :
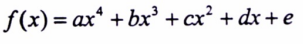
حيث إن : a, b, c, d, e ثوابت حقيقية.
5- كثير حدود من الدرجة الخامسة :
polynomial Function of the Fifth Degree
هي كثير حدود صيغتها العامة من الشكل :

حيث إن : a, b, c, d, e, f ثوابت حقيقية.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


