المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Tychonoff Plank |
 1315
 05:48 مساءً
date: 7-8-2021 |
Author : Kelley, J. L 
Book or Source : General Topology. New York: Van Nostrand, 
Page and Part : ...A Tychonoff plank is a topological space that is an example of a normal space which has a non-normal subset, thus showing that normality is not a hereditary property. Let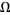 
be the set of all ordinals which are less than or equal to 
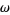, and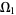 
the set of all ordinals which are less than or equal to 
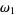. Consider the set 
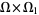with the product topology induced by the order topologies of 
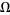and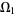 
. Then 
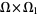is normal, but the subset 
is not. It can be shown that the set 
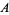of all elements of 
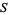whose first coordinate is equal to 
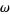and the set 
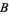of all elements of 
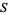whose second coordinate is equal to 
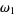are disjoint closed subsets 
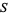, but there are no disjoint open subsets 
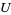and 
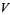of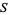 
such that 
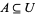and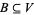 
.
REFERENCES:
Kelley, J. L. General Topology. New York: Van Nostrand, p. 132, 1955.
Willard, S. General Topology. Reading, MA: Addison-Wesley, pp. 122-123, 1970.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|
