Kontsevich's integral is a far-reaching generalization of the Gauss integral for the linking number, and provides a tool to construct the universal Vassiliev invariant of a knot. In fact, any Vassiliev knot invariant can be derived from it.

To construct the Kontsevich integral, represent the three-dimensional space 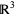 as a direct product of a complex line  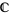with coordinate  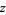and a real line  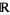with coordinate 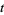. The integral is defined for Morse knots, i.e., knots  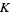embedded in  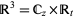in such a way that the coordinate  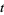is a Morse function on 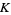, and its values belong to the graded completion  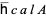of the algebra of chord diagrams .

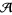The Kontsevich integral 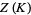 of the knot  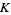is defined as

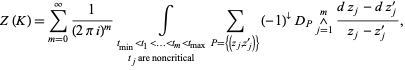(1)

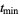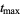where the ingredients of this formula have the following meanings. The real numbers  and  are the minimum and the maximum of the functi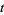on  on .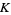

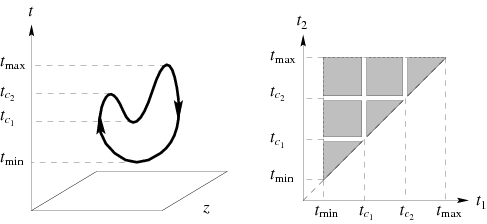
The integration domain is the 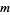-dimensional simplex  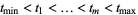divided by the critical values into a certain number of connected components. For example, for the embedding of the unknot and  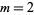(left figure), the corresponding integration domain has six connected components, illustrated in the right figure above.

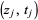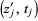The number of addends in the integrand is constant in each connected component of the integration domain, but can be different for different components. In each plane {t=t_j} subset R^3" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline21.gif" style="height:21px; width:72px" />, choose an unordered pair of distinct points  and  on 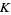 so that  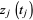and 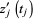 are continuous functions. Denote by  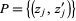the set of such pairs for 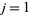, ..., 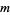, then the integrand is the sum over all choices of 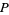. In the example above, for the component {t_(min)<t_1<t_(c_1),t_(c_2)<t_2<t_(max)}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline31.gif" style="height:21px; width:170px" />, we have only one possible pair of points on the levels {t=t_1}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline32.gif" style="height:15px; width:41px" /> and {t=t_2}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline33.gif" style="height:15px; width:41px" />. Therefore, the sum over 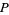 for this component consists of only one addend. In contrast, in the component {t_(min)<t_1<t_(c_1),t_(c_1)<t_2<t_(c_2)}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline35.gif" style="height:21px; width:163px" />, we still have only one possibility for the level {t=t_1}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline36.gif" style="height:15px; width:41px" />, but the plane {t=t_2}" src="https://mathworld.wolfram.com/images/equations/KontsevichIntegral/Inline37.gif" style="height:15px; width:41px" /> intersects our knot 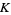 in four points. So we have  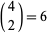possible pairs 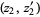, and the total number of addends is six (see the picture below).

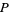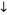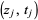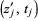For a pairing  the symbol '' denotes the number of points  or  in 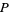 where the coordinate  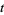decreases along the orientation of .

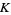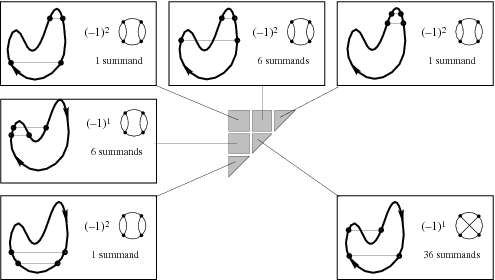
Fix a pairing 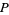, consider the knot  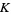as an oriented circle, and connect the points  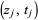and 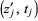 by a chord to obtain a chord diagram with  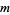chords. The corresponding element of the algebra  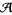is denoted 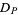. In the picture above, one of the possible pairings, the corresponding chord diagram with the sign 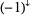, and the number of addends of the integrand (some of which are equal to zero in  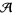due to a one-term relation) are shown for each connected component.

Over each connected component, 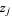 and 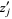 are smooth functions in 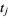. By  we mean the pullback of this form to the integration domain of variables 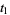, ..., 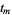. The integration domain is considered with the manifold orientation of the space  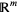defined by the natural order of the coordinates , ..., .

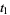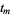By convention, the term in the Kontsevich integral corresponding to 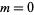 is the (only) chord diagram of order 0 with coefficient one. It represents the unit of the algebra .

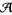The Kontsevich integral is convergent thanks to one-term relations. It is invariant under deformations of the knot in the class of Morse knots. Unfortunately, the Kontsevich integral is not invariant under deformations that change the number of critical points of the function 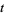. However, the formula shows how the integral changes under such deformations:

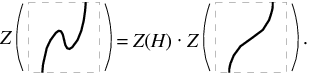
In the above equation, the graphical arguments of 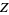 represent two embeddings of an arbitrary knot, differing only in the illustrated fragment,

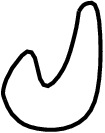
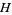 is the hump (i.e., the unknot embedded in  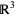in the specified way; illustrated above), and the product is the product in the completed algebra  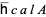of chord diagrams. The last equality allows the definition of the universal Vassiliev invariant by the formula

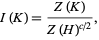(2)

where 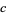 denotes the number of critical points of  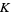and quotient means division in the algebra  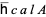according to the rule 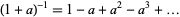. The universal Vassiliev invariant  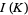is invariant under an arbitrary deformation of .

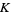Consider a function 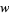 on the set of chord diagrams with  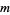chords satisfying one- and four-term relations (a weight system). Applying this function to the universal Vassiliev invariant 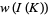, we get a numerical knot invariant. This invariant will be a Vassiliev invariant of order 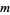, and any Vassiliev invariant can be obtained in this way.

The Kontsevich integral behaves in a nice way with respect to the natural operations on knots, such as mirror reflection, changing the orientation of the knot, and mutation of knots. In a proper normalization it is multiplicative under the connected sum of knots:

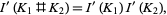(3)

where 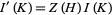. For any knot  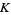the coefficients in the expansion of  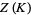over an arbitrary basis consisting of chord diagrams are rational (Kontsevich 1993, Le and Murakami 1996).

The task of computing the Kontsevich integral is very difficult. The explicit expression of the universal Vassiliev invariant 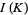 is currently known only for the unknot,

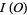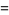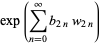			(4)
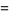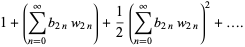			(5)

(Bar-Natan et al. 1995). Here, 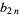 are modified Bernoulli numbers, i.e., the coefficients of the Taylor series

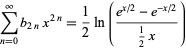(6)

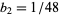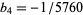(, , ...; OEIS A057868), and  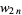are the wheels, i.e., diagrams of the form

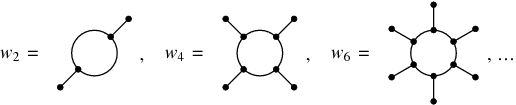
The linear combination is understood as an element of the algebra of Chinese characters 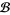, which is isomorphic to the algebra of chord diagrams 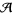. Expressed through chord diagrams, the beginning of this series looks as follows:

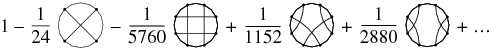
The Kontsevich integral was invented by Kontsevich (1993), and detailed expositions can be found in Arnol'd (1994), Bar-Natan (1995), and Chmutov and Duzhin (2000).

REFERENCES:

Arnol'd, V. I. "Vassiliev's Theory of Discriminants and Knots." In First European Congress of Mathematics, Vol. 1 (Paris, 1992) (Ed. A. Joseph, F. Mignot, F. Murat, B. Prum, and R. Rentschler). Basel, Switzerland: Birkhäuser, pp. 3-29, 1994.

Bar-Natan, D. "On the Vassiliev Knot Invariants." Topology 34, 423-472, 1995.

Bar-Natan, D.; Garoufalidis, S.; Rozansky, L.; and Thurston, D. "Wheels, Wheeling, and the Kontsevich Integral of the Unknot." Israel J. Math. 119, 217-237, 2000.

Chmutov, S. V. and Duzhin, S. V. "The Kontsevich Integral." Acta Appl. Math. 66, 155-190, 2000.

Kontsevich, M. "Vassiliev's Knot Invariants." Adv. Soviet Math. 16, Part 2, 137-150, 1993.

Le, T. Q. T. and Murakami, J. "The Universal Vassiliev-Kontsevich Invariant for Framed Oriented Links." Compos. Math. 102, 42-64, 1996.

Sloane, N. J. A. Sequence A057868 in "The On-Line Encyclopedia of Integer Sequences."

Vassiliev, V. A. "Cohomology of Knot Spaces." In Theory of Singularities and Its Applications (Ed. V. I. Arnold). Adv. Soviet Math. 1, 23-69, 1990.

اخر الاخبار

اخبار العتبة العباسية المقدسة

أهالي كربلاء يحيون اليوم السابع لذكرى شهادة الإمام الحسين (عليه السلام)

مشروع أمير القراء الوطني يشهد مشاركة أكثر من 100 طالبٍ في مرحلته الثالثة

قسم الشؤون الفكرية يصدر دليلًا يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة

قسم الشؤون الفكرية يعلن عن توفير عددٍ من المكتبات الإلكترونية المتخصّصة للمؤسّسات الدينية والمكتبات العامّة

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد