
Sheaf
 المؤلف:
Godement, R.
المؤلف:
Godement, R.
 المصدر:
Topologie Algébrique et Théorie des Faisceaux. Paris: Hermann, 1958.
المصدر:
Topologie Algébrique et Théorie des Faisceaux. Paris: Hermann, 1958.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 3-6-2021
3-6-2021
 2063
2063
Sheaf
A sheaf is a presheaf with "something" added allowing us to define things locally. This task is forbidden for presheaves in general. Specifically, a presheaf 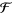 on a topological space
on a topological space 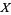 is a sheaf if it satisfies the following conditions:
is a sheaf if it satisfies the following conditions:
1. if 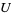 is an open set, if
is an open set, if ![<span style=]() {U_i}" src="https://mathworld.wolfram.com/images/equations/Sheaf/Inline4.gif" style="height:15px; width:24px" /> is an open covering of
{U_i}" src="https://mathworld.wolfram.com/images/equations/Sheaf/Inline4.gif" style="height:15px; width:24px" /> is an open covering of 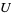 and if
and if 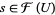 is an element such that
is an element such that 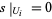 for all
for all 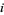 , then
, then 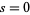 .
.
2. if 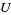 is an open set, if
is an open set, if ![<span style=]() {U_i}" src="https://mathworld.wolfram.com/images/equations/Sheaf/Inline11.gif" style="height:15px; width:24px" /> is an open covering of
{U_i}" src="https://mathworld.wolfram.com/images/equations/Sheaf/Inline11.gif" style="height:15px; width:24px" /> is an open covering of 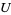 and if we have elements
and if we have elements 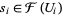 for each
for each 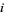 , with the property that for each,
, with the property that for each, 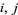 ,
, 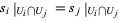 , then there is an element
, then there is an element 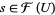 such that
such that 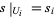 for all
for all 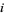 .
.
The first condition implies that 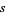 is unique.
is unique.
For example, let 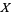 be a variety over a field
be a variety over a field 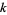 . If
. If 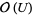 denotes the ring of regular functions from
denotes the ring of regular functions from 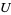 to
to 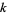 then with the usual restrictions
then with the usual restrictions 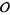 is a sheaf which is called the sheaf of regular functions on
is a sheaf which is called the sheaf of regular functions on 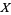 .
.
In the same way, one can define the sheaf of continuous real-valued functions on any topological space, and also for differentiable functions.
REFERENCES:
Godement, R. Topologie Algébrique et Théorie des Faisceaux. Paris: Hermann, 1958.
Hartshorne, R. Algebraic Geometry. New York: Springer-Verlag, 1977.
Iyanaga, S. and Kawada, Y. (Eds.). "Sheaves." §377 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1171-1174, 1980.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


