Morse Theory

A generalization of calculus of variations which draws the relationship between the stationary points of a smooth real-valued function on a manifold and the global topology of the manifold. For example, if a compact manifold admits a function whose only stationary points are a maximum and a minimum, then the manifold is a sphere. 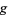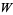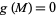Technically speaking, Morse theory applied to a function  on a manifold  with  and 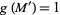 shows that every bordism can be realized as a finite sequence of surgeries. Conversely, a sequence of surgeries gives a bordism.

There are a number of classical applications of Morse theory, including counting geodesics on a Riemann surface and determination of the topology of a Lie group (Bott 1960, Milnor 1963). Morse theory has received much attention in the last two decades as a result of the paper by Witten (1982) which relates Morse theory to quantum field theory and also directly connects the stationary points of a smooth function to differential forms on the manifold.

REFERENCES:

Bott, R. Morse Theory and Its Applications to Homotopy Theory: Lectures by R. Bott. Bonn, Germany: Universität Bonn, 1960.

Chang, K. C. Infinite Dimensional Morse Theory and Multiple Solution Problems. Boston, MA: Birkhäuser, 1993.

Goresky, M. and MacPherson, R. Stratified Morse Theory. New York: Springer-Verlag, 1988.

Milnor, J. W. Morse Theory. Princeton, NJ: Princeton University Press, 1963.

Rassias, G. (Ed.). Morse Theory and Its Applications.

Veverka, J. F. The Morse Theory and Its Application to Solid State Physics. Kingston, Ontario, Canada: Queen's University, 1966.

Witten, E. "Supersymmetry and Morse Theory." J. Diff. Geom. 17, 661-692, 1982.