The fundamental group of an arcwise-connected set  is the group formed by the sets of equivalence classes of the set of all loops, i.e., paths with initial and final points at a given basepoint , under the equivalence relation of homotopy. The identity element of this group is the set of all paths homotopic to the degenerate path consisting of the point . The fundamental groups of homeomorphic spaces are isomorphic. In fact, the fundamental group only depends on the homotopy type of . The fundamental group of a topological space was introduced by Poincaré (Munkres 1993, p. 1).

The following is a table of the fundamental group for some common spaces , where  denotes the fundamental group,  is the first integral homology group,  denotes the group direct product,  denotes the free product,  denotes the ring of integers, and  is the cyclic group of order .

space ()	symbol
circle
complex projective space		0	0
figure eight
Klein bottle
-torus
real projective plane
sphere		0	0

The group product  of loop  and loop  is given by the path of  followed by the path of . The identity element is represented by the constant path, and the inverse of  is given by traversing  in the opposite direction. The fundamental group is independent of the choice of basepoint because any loop through  is homotopic to a loop through any other point . So it makes sense to say the "fundamental group of ."

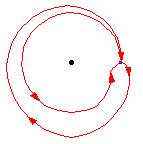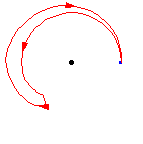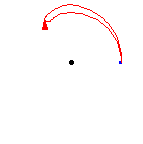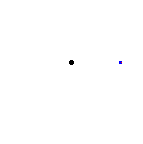
The diagram above shows that a loop followed by the opposite loop is homotopic to the constant loop, i.e., the identity. That is, it starts by traversing the path , and then turns around and goes the other way, . The composition is deformed, or homotoped, to the constant path, along the original path .

A space with a trivial fundamental group (i.e., every loop is homotopic to the constant loop), is called simply connected. For instance, any contractible space, like Euclidean space, is simply connected. The sphere is simply connected, but not contractible. By definition, the universal cover  is simply connected, and loops in  lift to paths in . The lifted paths in the universal cover define the deck transformations, which form a group isomorphic to the fundamental group.

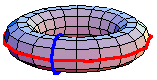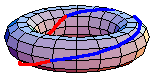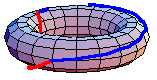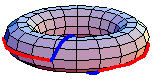
The underlying set of the fundamental group of  is the set of based homotopy classes from the circle to , denoted . For general spaces  and , there is no natural group structure on , but when there is,  is called a co-H-space. Besides the circle, every sphere  is a co-H-space, defining the homotopy groups. In general, the fundamental group is non-Abelian. However, the higher homotopy groups are Abelian. In some special cases, the fundamental group is Abelian. For example, the animation above shows that  in the torus. The red path goes before the blue path. The animation is a homotopy between the loop that goes around the inside first and the loop that goes around the outside first.

Since the first integral homology  of  is also represented by loops, which are the only one-dimensional objects with no boundary, there is a group homomorphism

which is surjective. In fact, the group kernel of  is the commutator subgroup and  is called Abelianization.

The fundamental group of  can be computed using van Kampen's theorem, when  can be written as a union  of spaces whose fundamental groups are known.

When  is a continuous map, then the fundamental group pushes forward. That is, there is a map  defined by taking the image of loops from . The pushforward map is natural, i.e.,  whenever the composition of two maps is defined.

REFERENCES:

Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2006.

Munkres, J. R. Elements of Algebraic Topology. New York: Perseus Books Pub., 1993.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد