
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
STATISTICAL MECHANICS OF BOSONS AND FERMIONS
المؤلف:
Thomas Banks
المصدر:
Quantum Mechanics
الجزء والصفحة:
264
28-3-2021
2565
STATISTICAL MECHANICS OF BOSONS AND FERMIONS
The most general system of noninteracting particles will have a variety of single particle energy eigenstates, labeled by a parameter p, which can be discrete or continuous and range over a finite or infinite number of values. The space of p values might also have a geometrical structure corresponding to some number of spatial dimensions. As an example, p could label both the three vector momentum P and the J3 component of the spin σ of a nonrelativistic particle of any spin j. The momentum would be discrete if space were a torus, and would live on a torus, the first Brillouin zone, if space were a lattice. Denote the energy of the p-th single particle state by ∈p.
The N-particle states are labeled by N copies of the quantum number p1, . . . pN, which are either symmetric or totally antisymmetric under permutations of the copies. The key to statistical mechanics is the realization that a nonredundant labeling of the states is just to give the number of particles n(p) occupying each single particle state p. For bosons, n(p) can be any nonnegative integer, while for fermions, it is either zero or one. For either type of statistics, we have
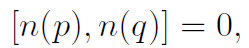
which means that the Hilbert space breaks up into a tensor product H = ⊗ pHp, where n(p) acts as 1 ⊗ . . . n(p) ⊗ 1 . . . ⊗ 1. That is, n(p) acts in a nontrivial way only on the factor Hp.
Furthermore, because p is a full set of single particle quantum numbers, the states in Hp are completely characterized by the eigenvalue of n(p). For fermions, Hp is two dimensional, while for bosons, it is infinite dimensional.
In nonrelativistic physics, the numbers of each type of stable elementary particle (electrons, protons, neutrons inside nuclei which do not undergo beta decay) are conserved quantum numbers. From a relativistic perspective, this is because we never consider transitions between energy levels differing by more than about 10−4 of the electron mass. For the purposes of this chapter, we will consider only a single type of elementary particle, so that there is only one such conserved quantum number
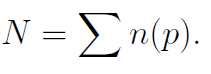
Conservation means that [N,H] = 0, which is evident from
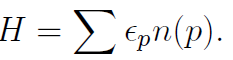
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















