
INTERFERENCE AND HUYGEN’S PRINCIPLE
 المؤلف:
George C. King
المؤلف:
George C. King
 المصدر:
Vibrations and Waves
المصدر:
Vibrations and Waves
 الجزء والصفحة:
163
الجزء والصفحة:
163
 6-2-2021
6-2-2021
 2633
2633
INTERFERENCE AND HUYGEN’S PRINCIPLE
Suppose that we have two monochromatic waves ψ1 and ψ2 with wavelength λ that have been derived from the same source: this avoids any random phase changes from two separate sources. These waves follow different paths and are recombined at a particular point in space. The difference in their path lengths from the common source is s. If this path difference is equal to an integral number of wavelengths, the crests and the troughs of one wave line up exactly with the crests and the troughs of the other wave, as shown in Figure 1(a): the two waves are said to be in phase. There is constructive interference and the amplitude of the superposition (ψ1 + ψ2) is equal to 2A where A is the amplitude of the individual waves. If the path difference is an odd number of half wavelengths, the crests of one wave line up with the troughs of the other wave as shown in Figure 2(b): the two waves are said to be out of phase. There is destructive interference and the amplitude of their superposition is zero. We write these interference
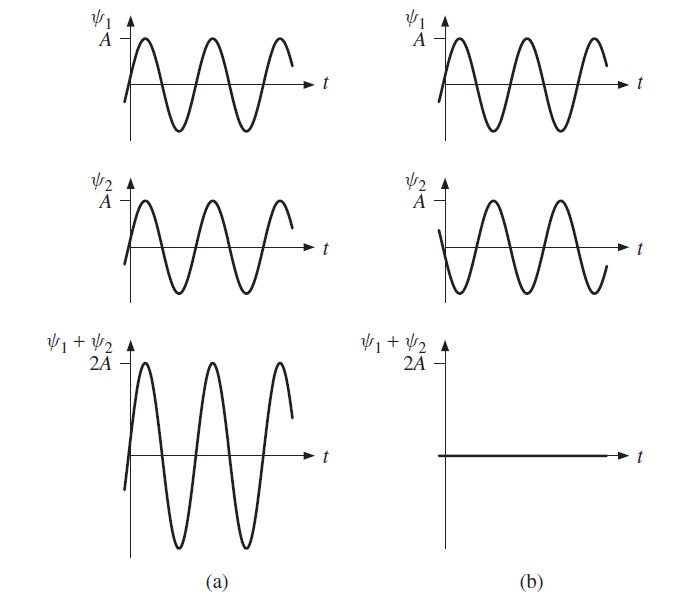
Figure 1 (a) Two monochromatic waves ψ1 and ψ2 at a particular point in space where the path difference from their common source is equal to an integral number of wavelengths. There is constructive interference and their superposition (ψ1 + ψ2) has an amplitude that is equal to 2A where A is the amplitude of the individual waves. (b) The two waves ψ1 and ψ2 where the path difference is equal to an odd number of half wavelengths. There is destructive interference and the amplitude of their superposition is zero.
conditions as:
 .......(1)
.......(1)
For other values of path difference s the resulting amplitude will lie between these two extremes of total constructive and destructive interference. Since phase difference Φ = 2πs/λ, we can also write the interference conditions as:
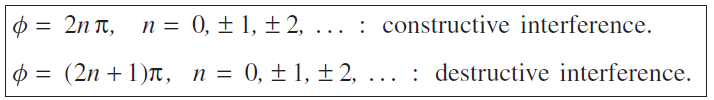 ......(2)
......(2)
These are the basic results for the interference of waves. They are of fundamental importance and can be applied to a wide range of physical phenomena. We shall apply them to various physical situations and in particular to an archetypal example of interference, namely Young’s double-slit experiment. This experiment incorporates all the essential physical principles of wave interference and we shall discuss it in some detail. However, before doing so, we first describe Huygen’s principle, which is named after the Dutch physicist Christian Huygen. This

Figure 2. The application of Huygen’s principle to the progression of a plane wave. Each point on the primary wavefront acts as a source of secondary wavelets. These secondary wavelets combine and their envelope represents the new wavefront, which is also a plane wave.
principle provides an empirical approach to predicting the progression of waves and we will use it to explain interference and, later, diffraction.
Huygen postulated that each point on a primary wavefront acts as a source of secondary wavelets such that the wavefront at some later time is the envelope of these wavelets. Huygen’s principle is illustrated in Figure 2 for the example of a plane wave. To construct the wavefront at a time interval Δt later, arcs are drawn in the forward direction from points across the primary wavefront. The radius of each arc is equal to vΔt where v is the wave velocity. These secondary wavelets combine and their envelope represents the new wavefront, which is also a plane wave as illustrated in Figure 2. If a wavefront encounters an aperture in an opaque barrier, the points on the wavefront across the aperture act like sources of secondary wavelets. When the aperture is very narrow, i.e. its width is comparable with the wavelength, the aperture acts like a point source and wavelets spread out in a semicircular fashion, as illustrated in Figure 3. The effect of the barrier is to suppress all propagation of the primary wave except through the aperture. Huygen’s principle is successful in describing, at least qualitatively, the behaviour of the waves in these two examples. It is important to note, however, that Huygen’s principle is an empirical approach. It provides only a qualitative description of the progression of a wave and it has shortcomings. In particular, we would expect the secondary sources on the primary wavefront to also produce a wave that propagates in the backward direction. In reality this does not occur and Huygen’s principle ignores this other wavefront. However, a full and rigorous treatment of wave propagation, subsequently developed by G. Kirchhoff, finds that the secondary wavelets do in fact lie in the forward direction.
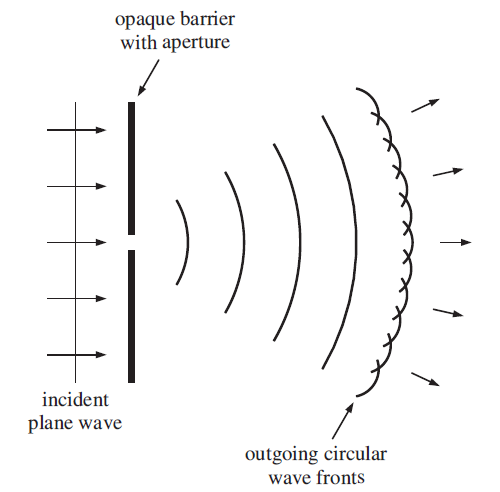
Figure 3 When a wavefront encounters an aperture in an opaque barrier, the barrier suppresses all propagation of the wave except through the aperture. Following Huygen’s principle, the points on the wavefront across the aperture act as sources of secondary wavelets. When the width of the aperture is comparable with the wavelength, the aperture acts like a point source and the outgoing wavefronts are semicircular.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


