Heavy damping

Heavy damping occurs when the degree of damping is sufficiently large that the system returns sluggishly to its equilibrium position without making any oscillations at all. This corresponds to the mass in Figure 1.1 being immersed in a fluid of large viscosity like syrup. For this case the oscillatory part of our solution, cos ωt in Equation (2.1), is no longer appropriate. Instead we replace it with the general function f (t), i.e.

x = exp(−βt)f (t ). .........(1)

Substituting x and its derivatives into letting β = γ/2 gives

.........(2)

or

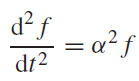............(3)

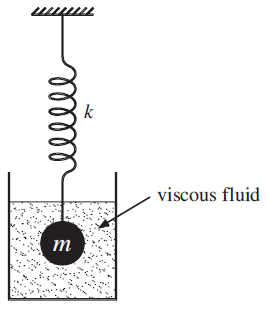
Figure 1.1 An example of a damped mechanical oscillator showing an oscillating mass immersed in a viscous fluid.

where α² = (γ ²/4 − ω²_o). The solutions to Equation (3) depend dramatically on the sign of α². The α² term is negative when γ ²/4 < ω²_o and this leads to an oscillatory solution with the complex form f (t) = Aexp i(αt + φ). This solution is not appropriate for the case of heavy damping where there is no oscillation. In fact it corresponds to the case of light damping. The α² term is positive when γ ²/4>ω²_o. In this case Equation (3) has the general solution

f (t) = Aexp(αt) + B exp(−αt),

giving
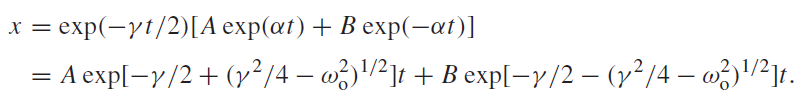........(4)
This is the non-oscillatory solution that we require. The term (γ ²/4 − ω²_o)^1/2 is clearly less than γ/2 and so the exponents of both exponential terms are negative in sign. Hence the displacement reduces to zero with time and there is no oscillation.

اخر الاخبار

اخبار العتبة العباسية المقدسة

ما الخدمات التي قدّمها موكب أشبال الطفّ لزائري عاشوراء؟

العتبة العباسية المقدسة تنظّم مسيرات عزائية لإحياء ذكرى عاشوراء في نينوى

قسم الشؤون الفكرية يحيي ذكرى استشهاد الإمام الحسين (عليه السلام) في القارة الإفريقية

قسمُ التربية والتعليم يقيم مجلسه العزائي السنوي بذكرى عاشوراء

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد

مواضيع ذات صلة

لعبة عجلة الجاذبية الأرضية

بعض الأرقام القياسية لعلامات الاحتكاك

الاختيار بين الانزلاق وعدم الانزلاق

نقار الخشب وكبش الجبال الصخرية وارتجاج المخ

انزلاق الإطارات على الطريق

اجتياز الضوء الأصفر

دوران السيارة حول نفسها بسبب الضغط المفاجئ على المكابح

اللاتناظر الزمني والحركة الموجية (اللاتناظر الزمني في الأمواج: من بحيرة ساكنة إلى الكون اللامتناهي)

القوافل والاختناقات المرورية

الحد الأدنى للمسافة الفاصلة بين السيارات(خرافة المسافة الآمنة: الفيزياء تكشف خطأ القاعدة التقليدية)

موجات الصدمة على الطريق السريع

الركض أم السير تحت الأمطار ؟(عندما تلتقي قطرات المطر مع قوانين الفيزياء)