NSW Number
المؤلف:
Newman, M.; Shanks, D.; and Williams, H. C.
المصدر:
"Simple Groups of Square Order and an Interesting Sequence of Primes." Acta Arith. 38
الجزء والصفحة:
...
5-1-2021
1434
NSW Number
An NSW number (named after Newman, Shanks, and Williams) is an integer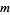 
that solves the Diophantine equation
 |
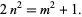(1)
|
In other words, the NSW numbers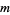 
index the diagonals of squares of side length 
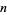having the property that the squares of the diagonal 
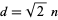equals one plus a square number 
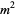. Such numbers were called "rational diagonals" by the Greeks (Wells 1986, p. 70). The name "NSW number" derives from the names of the authors of the paper on the subject written by Newman et al. (1980/81).
The first few NSW numbers are therefore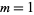 
, 7, 41, 239, 1393, ... (OEIS A002315), which correspond to square side lengths 
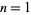, 5, 29, 169, 985, 5741, 33461, 195025, ... (OEIS A001653). The values indexed by 
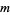and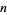 
therefore give 2, 50, 1682, 57122, ... (OEIS A088920).
Taking twice the NSW numbers gives the sequence 2, 14, 82, 478, 2786, 16238, ... (OEIS A077444), which is exactly every other Pell-Lucas number.
The first few prime NSW numbers are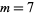 
, 41, 239, 9369319, 63018038201, 489133282872437279, ... (OEIS A088165), corresponding to indices 
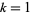, 2, 3, 9, 14, 23, 29, 81, 128, 210, 468, 473, 746, 950, 3344, 4043, 4839, 14376, 39521, 64563, 72984, 82899, 84338, 85206, 86121, ... (OEIS A113501).
The following table summarizes the largest known NSW primes, where the indices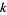 
correspond via 
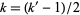to the indices 
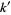of prime half-Pell-Lucas numbers that are odd.
 |
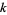decimal digits |
discoverer |
date |
 |
 |
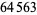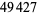E. W. Weisstein |
May 19, 2006 |
 |
 |
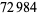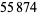E. W. Weisstein |
Aug. 29, 2006 |
 |
 |
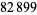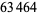E. W. Weisstein |
Nov. 16, 2006 |
 |
 |
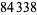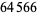E. W. Weisstein |
Nov. 26, 2006 |
 |
 |
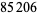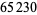E. W. Weisstein |
Dec. 10, 2006 |
 |
 |
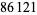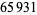E. W. Weisstein |
Jan. 25, 2007 |
Interestingly, the values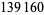 
give every other convergent to Pythagoras's constant 
.
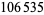Explicit formula for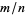 
and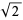 
are given by
for positive integers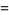 
(Ribenboim 1996, p. 367). A recurrence relation for 
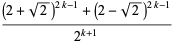is given by
 |
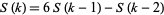(4)
|
with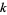 
and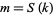 
.
REFERENCES:
Newman, M.; Shanks, D.; and Williams, H. C. "Simple Groups of Square Order and an Interesting Sequence of Primes." Acta Arith. 38, 129-140, 1980/81.
Ribenboim, P. "The NSW Primes." §5.9 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 367-369, 1996.
Sloane, N. J. A. Sequences A001653/M3955, A002315/M4423, A077444, A088165, A088920, and A113501 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
