Binomial Number

A binomial number is a number of the form 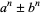, where 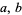, and 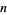 are integers. Binomial numbers can be factored algebraically as

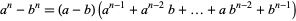(1)

for all ,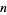

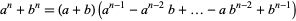(2)

for 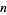 odd, and

(3)

for all positive integers 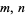. For example,

			(4)
			(5)
			(6)
			(7)
			(8)
			(9)
			(10)
			(11)
			(12)

and

			(13)
			(14)
			(15)
			(16)
			(17)
			(18)
			(19)
			(20)
			(21)

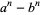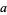Rather surprisingly, the number of factors of  with  and 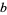 symbolic and  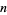a positive integer is given by 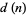, where  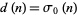is the number of divisors of  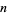and 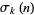 is the divisor function. The first few terms are therefore 1, 2, 2, 3, 2, 4, 2, ... (OEIS A000005).

Similarly, the number of factors of 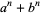 is given by 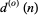, where  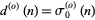is the number of odd divisors of  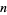and 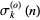 is the odd divisor function. The first few terms are therefore 1, 1, 2, 1, 2, 2, 2, 1,... (OEIS A001227).

In 1770, Euler proved that if 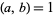, then every odd factor of

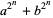(22)

is of the form 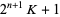. (A number of the form  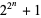is called a Fermat number.)

If 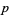 and 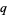 are primes, then

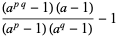(23)

is divisible by every prime factor of 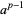 not dividing .

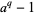REFERENCES:

Guy, R. K. "When Does 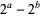 Divide 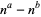." §B47 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 102, 1994.

Qi, S and Ming-Zhi, Z. "Pairs where 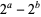 Divides  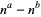for All 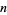." Proc. Amer. Math. Soc. 93, 218-220, 1985.

Schinzel, A. "On Primitive Prime Factors of 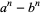." Proc. Cambridge Phil. Soc. 58, 555-562, 1962.

Sloane, N. J. A. Sequences A000005/M0246 and A001227 in "The On-Line Encyclopedia of Integer Sequences."