Sierpiński Constant
المؤلف:
Finch, S. R.
المصدر:
Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
الجزء والصفحة:
...
28-12-2020
1380
Sierpiński Constant
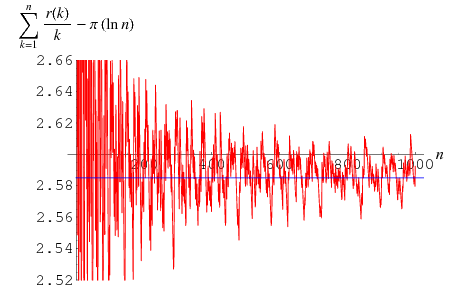
Let the sum of squares function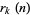 
denote the number of representations of 
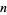by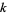 
squares, then the summatory function of 
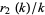has the asymptotic expansion
 |
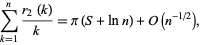(1)
|
where
(OEIS A241017) is the Sierpiński constant (Finch 2003, p. 123),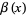 
is the Dirichlet beta function, 
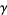is the Euler-Mascheroni constant, and 
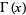is the gamma function.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 114, 2003.
Sierpiński, W. Oeuvres Choisies, Tome 1. Editions Scientifiques de Pologne, 1974.
Sloane, N. J. A. Sequences A062089 and A241017 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
